具有固定批次因子的稳定性研究示例

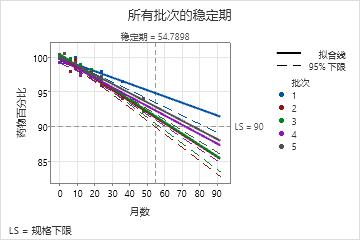
一家制药公司的质量工程师想要确定包含新药物的药丸的保质期。药丸中药物的浓度会随着时间的推移而降低。该工程师想要确定药丸何时达到预期浓度的 90%。由于这是新药物，因此该公司只有 5 个中试批次可用来估计保质期。工程师在九个不同的时间检验每个批次中的一个药丸。

为了估计保质期，工程师将执行稳定性研究。由于工程师抽取了所有批次，因此批次是固定因子，而不是随机因子。

打开样本数据稳定期.MTW。
选择统计 > 回归 > 稳定性研究 > 稳定性研究。
在响应中，输入药物百分比。
在时间中，输入月数。
在批次中，输入批次。
在规格下限中，输入 90。
单击图形。
在稳定期图下的第二个下拉列表中，选择各个批次都没有图形。
在残差图下，选择四合一。
单击每个对话框中的确定。

解释结果

要遵循人用药注册技术要求国际协调会议 (ICH) 的 2003 条准则，工程师为要包括在模型中的项选择的 P 值为 0.25。“月份*批次”交互作用项的 P 值为 0.048。由于 P 值小于显著性水平 0.25，因此工程师断定每个批次的回归方程中的斜率都不同。批次 3 具有最大斜率 -0.1630，这表示批次 3 的浓度下降得最快。批次 2 具有最短保质期 54.79，因此整体保质期就是批次 2 的保质期。

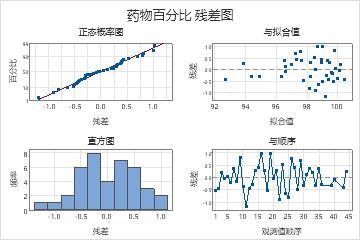
残差足够正态化，并且随机分散在 0 附近。在残差与拟合值图上，图左侧的点比右侧的少。之所以出现此模式，是因为质量工程师在研究的早期（浓度较高时）收集的数据较多。此模式不违反分析假设。

来源	自由度	Seq SS	Seq MS	F 值	P 值
月数	1	122.460	122.460	345.93	0.000
批次	4	2.587	0.647	1.83	0.150
月数*批次	4	3.850	0.962	2.72	0.048
误差	30	10.620	0.354
合计	39	139.516

项	系数	系数标准误	T 值	P 值	方差膨胀因子
常量	100.085	0.143	701.82	0.000
月数	-0.13633	0.00769	-17.74	0.000	1.07
批次
1	-0.232	0.292	-0.80	0.432	3.85
2	0.068	0.292	0.23	0.818	3.85
3	0.394	0.275	1.43	0.162	3.41
4	-0.317	0.292	-1.08	0.287	3.85
5	0.088	0.275	0.32	0.752	*
月数*批次
1	0.0454	0.0164	2.76	0.010	4.52
2	-0.0241	0.0164	-1.47	0.152	4.52
3	-0.0267	0.0136	-1.96	0.060	3.65
4	0.0014	0.0164	0.08	0.935	4.52
5	0.0040	0.0136	0.30	0.769	*

观测值	药物百分比	拟合值	残差	标准化残差
11	98.001	99.190	-1.189	-2.21	R
43	92.242	92.655	-0.413	-1.47		X
44	94.069	93.823	0.246	0.87		X

批次	稳定期
1	83.552
2	54.790
3	57.492
4	60.898
5	66.854
整体	54.790

具有固定批次因子的稳定性研究示例

解释结果

方法

因子信息

模型选择，α = 0.25

模型汇总

系数

回归方程

异常观测值的拟合和诊断

估计稳定期

批次
1	药物百分比	=	99.853 - 0.0909 月数

2	药物百分比	=	100.153 - 0.1605 月数

3	药物百分比	=	100.479 - 0.1630 月数

4	药物百分比	=	99.769 - 0.1350 月数

5	药物百分比	=	100.173 - 0.1323 月数