请选择您所选的方法或公式。
系数和标准化系数
系数是回归方程中的参数。可以同时使用估计系数和预测变量来计算响应变量的拟合值和新观测值的预测响应。与最小二乘不同,PLS 系数是非线性估计量。标准化系数表示模型中每个预测变量的重要性,并且对应于标准化 X 和 Y 变量。在 PLS 中,系数矩阵(维度 p × r)是根据权重和载荷计算的。
标准化系数的公式为:

要计算非标准化系数和截距,请使用以下公式:
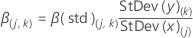

表示法
| 项 | 说明 |
|---|---|
| W | X 权重矩阵 |
| P | X 载荷矩阵 |
| C | Y 载荷矩阵 |
| j | 预测变量 (1, p) |
| k | 响应变量 (1, r) |
| p | 预测变量数 |
| r | 响应变量数 |
杠杆率
在最小二乘回归中,杠杆率是表示相应观测值与 X 空间中心的距离的值,使用 X 值描述。在 PLS 中,预测变量会被 X 分值替换。高杠杆率的观测值具有远离零点的 X 分值,对回归系数有显著影响。高杠杆率的点是 X 空间中的异常值,但不一定是 Y 空间中的异常值。
会根据 X 分值矩阵 T 计算 PLS 中的杠杆率值,X 分值矩阵 T 可用于计算帽子矩阵 (H),如下所示:

第 i 个观测值的杠杆率 (hii) 是 H 矩阵的第 i 个对角线元素。
大于 2m/n 的杠杆率值被视为较高值,并且应进行检查。
表示法
| 项 | 说明 |
|---|---|
| n | 观测值数 |
| m | 分量数 |
距 X 模型的距离
度量 X 空间中的观测值的拟合优度;表示 X 分值描述观测值的准确程度。距离很大的观测值也可能是杠杆率点。
公式
为第 i 个观测值计算与 X 模型的距离的公式如下所示:
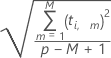
表示法
| 项 | 说明 |
|---|---|
| M | 分量数 |
| t | X 分值 |
| p | 预测变量数 |
距 Y 模型的距离
度量 Y 空间中的观测值的拟合优度;表示 Y 分值描述观测值的准确程度。距离很大的观测值也可能是异常值。
公式
为第 i 个观测值计算与 Y 模型的距离的公式如下所示:
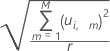
表示法
| 项 | 说明 |
|---|---|
| M | 分量数 |
| u | Y 分值 |
| r | 响应变量数 |
