步骤 1. 确定模型中的分量数
使用 PLS 的目标是要选择一个具有相应分量数且具备良好预测能力的模型。当您拟合 PLS 模型时,您可以执行交叉验证以帮助您确定模型最优的分量数。对于交叉验证,Minitab 会选择 R2 值最高的模型。如果您不使用交叉验证,您可以指定模型中要包括的分量数或使用默认分量数。默认分量数为 10 或数据中的预测变量数(以较小者为准)。检查方法表以确定 Minitab 包括在模型中的分量数。您还可以检查模型选择图。
在使用 PLS 时,选择一个模型,其中包含为了解释预测变量和响应中足够数量的变异性而所需的最小分量数。要确定最适合您的数据的分量数,请检查模型选择表(包括 X 方差、R2 和预测 R2 值)。预测 R2 指示模型的预测能力,而且仅在执行交叉验证时显示。
在某些情况下,您可能会决定使用最初由 Minitab 所选择的模型之外的其他模型。如果您使用交叉验证,请比较 R2 和预测 R2。例如,从 Minitab 只轻微降低预测 R2 的模型中删除两个分量。由于预测 R2 只是轻微降低,因此该模型不会过度拟合,且可以确定它比较适合您的数据。
实质上小于 R2 的预测的 R2 可能表明模型过度拟合。在向总体中添加不太重要的影响项或分量的情况下(尽管它们在样本数据中看起来比较重要),可能会发生过度拟合模型。模型针对样本数据而定制,因此可能对于总体预测不太有效。
如果您不使用交叉验证,可以检查模型选择表中的 X 方差值,以确定响应中由每个模型解释的方差量。
方法
| 交叉验证 | 逐一剔除法 |
|---|---|
| 要估算的分量 | 集合 |
| 已估算的分量数 | 10 |
| 已选定的分量数 | 4 |
方法
| 交叉验证 | 无 |
|---|---|
| 要计算的分量 | 集合 |
| 已计算的分量数 | 10 |
主要结果:分量数
在这些结果中,在第一个方法表中使用交叉验证而且选择了具有 4 个分量的模型。在第二个方法表中,未使用交叉验证。Minitab 使用具有 10 个(默认值)分量的模型。
芳香度 的模型选择和验证
| 分量 | X 方差 | 误差 | R-Sq | PRESS | R-Sq(预测) |
|---|---|---|---|---|---|
| 1 | 0.158849 | 14.9389 | 0.637435 | 23.3439 | 0.433444 |
| 2 | 0.442267 | 12.2966 | 0.701564 | 21.0936 | 0.488060 |
| 3 | 0.522977 | 7.9761 | 0.806420 | 19.6136 | 0.523978 |
| 4 | 0.594546 | 6.6519 | 0.838559 | 18.1683 | 0.559056 |
| 5 | 5.8530 | 0.857948 | 19.2675 | 0.532379 | |
| 6 | 5.0123 | 0.878352 | 22.3739 | 0.456988 | |
| 7 | 4.3109 | 0.895374 | 24.0041 | 0.417421 | |
| 8 | 4.0866 | 0.900818 | 24.7736 | 0.398747 | |
| 9 | 3.5886 | 0.912904 | 24.9090 | 0.395460 | |
| 10 | 3.2750 | 0.920516 | 24.8293 | 0.397395 |
主要结果:X 方差、R-sq、R-sq(预测)
在这些结果中,Minitab 选择了预测 R2 值近似 56% 的 4 分量模型。根据 X 方差,4 分量模型可解释预测变量中将近 60% 的方差。当分量数增加时,R2 值也会增加,但预测 R2 会降低,这表示分量较多的模型很可能会过度拟合。
步骤 2. 确定数据中是否包含异常值或杠杆率点
要确定模型是否可以很好地拟合数据,您需要检查残差图以找出异常值、杠杆率点及其他模式。如果数据中包含多个异常值或杠杆率点,则该模型无法提供有效的预测。
- 异常值:标准化残差较大的观测值在图中位于水平参考线之外。
- 杠杆率点:具有杠杆率值的观测值,其 X 分值远离零点且位于垂直参考线的右侧。
有关残差与杠杆率图的更多信息,请转到偏最小二乘回归的图形。
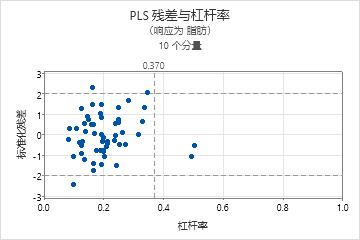
- 这些点中的非线性模式,表明模型不能很好地拟合或预测数据。
- 执行交叉验证时,如果拟合值与交叉验证的值之间存在较大差异,则表明存在杠杆率点。
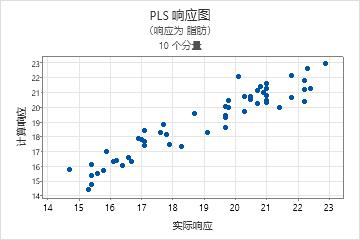
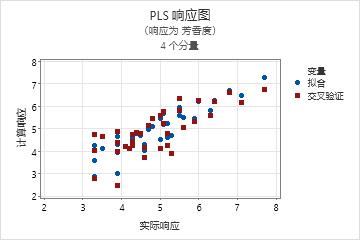
步骤 3. 使用检验数据集验证 PLS 模型
通常,执行 PLS 回归有两个步骤。第一个步骤有时称为培训,是计算样本数据集(又称培训数据集)的 PLS 回归模型。第二个步骤是用另一个数据集(通常称为检验数据集)验证此模型。要用检验数据集验证模型,请在预测子对话框中输入多列检验数据。Minitab 会为检验数据集中的每个观测值计算新响应值,并将预测响应与实际响应进行比较。Minitab 会根据比较结果计算检验 R2,该值表示模型预测新响应的能力。检验 R 2 值越大,模型的预测能力越强。
如果使用交叉验证,请比较检验 R2 和预测的 R2。理想情况下,这些值应该相近。如果检验 R2 明显小于预测的 R2,则表明交叉验证对模型的预测能力过于乐观,或两个数据样本来自不同的总体。
如果检验数据集不包括响应值,则 Minitab 不会计算检验 R2。
使用 脂肪 模型对新观测值的预测响应
| 行 | 拟合值 | 拟合值标准误 | 95% 置信区间 | 95% 预测区间 |
|---|---|---|---|---|
| 1 | 18.7372 | 0.378459 | (17.9740, 19.5004) | (16.8612, 20.6132) |
| 2 | 15.3782 | 0.362762 | (14.6466, 16.1098) | (13.5149, 17.2415) |
| 3 | 20.7838 | 0.491134 | (19.7933, 21.7743) | (18.8044, 22.7632) |
| 4 | 14.3684 | 0.544761 | (13.2698, 15.4670) | (12.3328, 16.4040) |
| 5 | 16.6016 | 0.348485 | (15.8988, 17.3044) | (14.7494, 18.4538) |
| 6 | 20.7471 | 0.472648 | (19.7939, 21.7003) | (18.7861, 22.7080) |
主要结果:R2
在这些结果中,检验 R2 约为 76%。原始数据集的预测 R2 约为 78%。由于这些值相似,因此您可以断定该模型具有足够的预测能力。
