拟合值
拟合值又称拟合或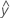 
。拟合值是对于给定预测变量值的均值响应的点估计。这些预测变量值又称 X 值。
解释
拟合值是通过将数据集内每个观测值的特定 x 值输入到模型方程中来计算的。
例如，如果方程为 y = 5 + 10x，则 x 值 2 的拟合值为 25 (25 = 5 + 10(2))。
拟合值 SE
拟合值标准误（拟合值 SE）用于估计指定变量设置的估计平均响应中的变异。将使用拟合值标准误来计算平均响应的置信区间。标准误始终为非负值。
解释
使用拟合值标准误可度量平均响应估计值的精确度。标准误越小，预测平均响应越精确。例如，一位分析人员设计了一个用于预测交货时间的模型。对于一组变量设置，该模型预测平均交货时间为 3.80 天。这些设置的拟合值标准误为 0.08 天。对于第二组变量设置，模型生成了相同的平均交货时间，但是拟合值标准误为 0.02 天。该分析人员可以确信：第二组变量设置的平均交货时间更接近 3.80 天。
您可以将拟合值标准误与拟合值结合使用，从而创建平均响应的置信区间。例如，根据自由度的数量，95% 置信区间将大约从预测均值上方和下方展开两个标准误。对于交货时间，当标准误为 0.08 时，预测均值 3.80 天的 95% 置信区间为 (3.64, 3.96) 天。总体均值在此范围内的置信度为 95%。当标准误为 0.02 时，95% 置信区间为 (3.76, 3.84) 天。第二组变量设置的置信区间更窄，因为其标准误较小。
95% 置信区间
在指定的预测变量设置条件下，拟合值的置信区间为均值响应提供可能值的范围。
解释
使用置信区间为变量的观测值评估拟合值的估计值。
例如，对于 95% 置信区间，置信区间包含模型中指定变量值的总体均值的可信度为 95%。该置信区间有助于评估结果的实际意义。使用您的专业知识可以确定置信区间是否包括对您的情形有实际意义的值。置信区间越宽，未来值的平均值的可信度越低。如果区间因太宽而毫无用处，请考虑增加样本数量。
95% PI
预测区间是可能包含预测变量值的一个未来响应变量的极差。
解释
对于 95% 置信区间，新观测值落入该区间内的可信度为 95%。（但是，请注意，这只对包含在分析的数据极差内的值才有效。）该区间由下限和上限共同定义，它们可由预测值的置信水平和标准误计算得出。预测区间总是要比置信区间大，这是因为在对单个响应与均值响应的预测中包括了更多的不确定性。
检验 R 平方
检验 R2 表示响应中由原始模型使用来自检验数据的预测变量值解释的变异的比率。
检验数据集必须包括与原始数据集相同数量的预测变量。只有检验数据包括每个观测值的响应数据时，才能计算检验 R2。检验 R2 的计算方法与 R2 的相同。
解释
检验 R2 可确定 PLS 回归模型预测检验数据的优度。检验 R2 值越高表明模型的预测能力越强。
通常，使用两个步骤执行 PLS 回归。第一个步骤有时称为培训，是计算样本数据集（又称培训数据集）的 PLS 回归模型。第二个步骤是用另一个数据集（通常称为检验数据集）验证此模型。某些检验数据集包括响应值，其他则不包括。如果检验数据集包括响应值，则 Minitab 可以计算检验 R2。
如果使用交叉验证，请比较检验 R2 和预测的 R2。理想情况下，这些值应该相近。如果检验 R2 明显小于预测的 R2，则表明交叉验证对模型的预测能力过于乐观，或两个数据样本来自不同的总体。
