一位葡萄酒制造商想了解葡萄酒中的化学成分与感官评价之间的关系。他有 37 个 Pinot Noir 样本,每个样本都由 17 种元素浓度(Cd、Mo、Mn、Ni、Cu、Al、Ba、Cr、Sr、Pb、B、Mg、Si、Na、Ca、P、K)和一组评审员根据葡萄酒的芳香度给出的分值描述。他想根据这 17 种元素浓度预测芳香度分值。数据来源:I.E. Frank 和 B.R. Kowalski (1984)。“Prediction of Wine Quality and Geographic Origin from Chemical Measurements by Partial Least-Squares Regression Modeling”(通过偏最小二乘回归建模根据化学测量值预测葡萄酒质量和地理起源),Analytica Chimica Acta(分析化学学报),第 162 页和第 241 到 251 页。
该制造商想包含所有浓度和所有将镉 (Cd) 包含在模型中的双因子交互作用。由于预测变量的样本比率较低,因此制造商决定使用偏最小二乘回归。
- 打开样本数据 葡萄酒芳香度.MWX。
- 选择。
- 在响应中,输入芳香度。
- 在模型中,输入Cd-KCd*MoCd*MnCd*NiCd*CuCd*AlCd*BaCd*CrCd*SrCd*PbCd*BCd*MgCd*SiCd*NaCd*CaCd*PCd*K。
- 单击选项。
- 在交叉验证下,选择逐一剔除法。单击确定。
- 单击图形。选择模型选择图。取消选中响应图和系数图。
- 单击每个对话框中的确定。
解释结果
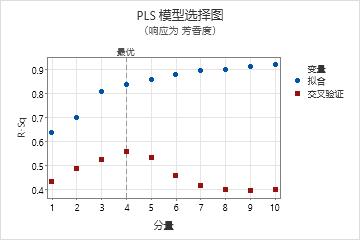
模型选择图会将具有 4 个分量的模型标识为最优模型,因为 4 分量模型的预测 R2 值最高。图中的预测 R2 值是使用交叉验证计算的。模型选择和验证表显示最优模型的预测 R2 值约为 0.56。Minitab 会将最优模型用于方差分析的计算。最优模型在显著性水平为 0.05 时具有统计显著性,因为 P 值约为 0.000。
方法
| 交叉验证 | 逐一剔除法 |
|---|---|
| 要估算的分量 | 集合 |
| 已估算的分量数 | 10 |
| 已选定的分量数 | 4 |
芳香度 的方差分析
| 来源 | 自由度 | SS | MS | F | P |
|---|---|---|---|---|---|
| 回归 | 4 | 34.5514 | 8.63784 | 41.55 | 0.000 |
| 残差误差 | 32 | 6.6519 | 0.20787 | ||
| 合计 | 36 | 41.2032 |
芳香度 的模型选择和验证
| 分量 | X 方差 | 误差 | R-Sq | PRESS | R-Sq(预测) |
|---|---|---|---|---|---|
| 1 | 0.158849 | 14.9389 | 0.637435 | 23.3439 | 0.433444 |
| 2 | 0.442267 | 12.2966 | 0.701564 | 21.0936 | 0.488060 |
| 3 | 0.522977 | 7.9761 | 0.806420 | 19.6136 | 0.523978 |
| 4 | 0.594546 | 6.6519 | 0.838559 | 18.1683 | 0.559056 |
| 5 | 5.8530 | 0.857948 | 19.2675 | 0.532379 | |
| 6 | 5.0123 | 0.878352 | 22.3739 | 0.456988 | |
| 7 | 4.3109 | 0.895374 | 24.0041 | 0.417421 | |
| 8 | 4.0866 | 0.900818 | 24.7736 | 0.398747 | |
| 9 | 3.5886 | 0.912904 | 24.9090 | 0.395460 | |
| 10 | 3.2750 | 0.920516 | 24.8293 | 0.397395 |