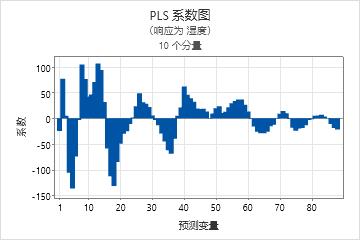
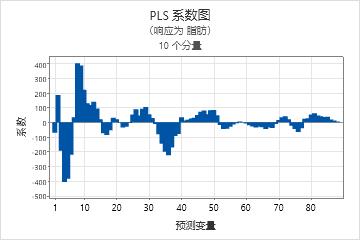
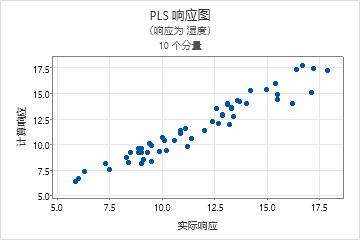
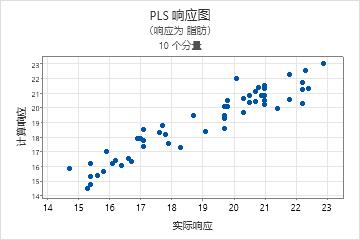
食品化学实验室的科学家分析 60 个豆粉样本。科学家确定每个样本的含水量和脂肪含量,并记录 88 个波长处的近红外 (NIR) 光谱数据。科学家从这 60 个样本中随机选择 54 个样本,并使用 PLS 回归来估计响应(含水量和脂肪)和预测变量(88 个 NIR 波长)之间的关系。科学家使用其余的 6 个样本作为检验数据集来评估模型的预测能力。
- 打开样本数据 大豆粉.MWX。
- 选择。
- 在响应中,输入湿度脂肪。
- 在模型中,输入“1'-'88”。
- 单击预测。
- 在连续预测变量的新观测值中,输入测试1-测试88。
- 在响应的新观测值 (可选)中,输入湿度2脂肪2。
- 单击每个对话框中的确定。
解释结果
两个响应变量的 P 值约为 0.000,该值小于显著性水平 0.05。这些结果指示模型中至少有一个系数不等于零。湿度的检验 R2 值约为 0.9。脂肪的检验 R2 值约为 0.8。检验 R2 统计量指示模型的预测效果良好。每个响应的分析分别提供不同的结果。
方法
| 交叉验证 | 无 |
|---|---|
| 要计算的分量 | 集合 |
| 已计算的分量数 | 10 |
湿度 的方差分析
| 来源 | 自由度 | SS | MS | F | P |
|---|---|---|---|---|---|
| 回归 | 10 | 468.516 | 46.8516 | 61.46 | 0.000 |
| 残差误差 | 43 | 32.777 | 0.7623 | ||
| 合计 | 53 | 501.293 |
脂肪 的方差分析
| 来源 | 自由度 | SS | MS | F | P |
|---|---|---|---|---|---|
| 回归 | 10 | 266.378 | 26.6378 | 36.89 | 0.000 |
| 残差误差 | 43 | 31.050 | 0.7221 | ||
| 合计 | 53 | 297.428 |
湿度 的模型选择和验证
| 分量 | X 方差 | 误差 | R-Sq |
|---|---|---|---|
| 1 | 0.984976 | 96.9288 | 0.806643 |
| 2 | 0.996400 | 88.9900 | 0.822479 |
| 3 | 0.997757 | 71.9304 | 0.856510 |
| 4 | 0.999427 | 58.3174 | 0.883666 |
| 5 | 0.999722 | 58.1261 | 0.884048 |
| 6 | 0.999853 | 48.5236 | 0.903203 |
| 7 | 0.999963 | 45.9824 | 0.908272 |
| 8 | 0.999976 | 33.1545 | 0.933862 |
| 9 | 0.999982 | 32.8074 | 0.934554 |
| 10 | 0.999986 | 32.7773 | 0.934615 |
脂肪 的模型选择和验证
| 分量 | X 方差 | 误差 | R-Sq |
|---|---|---|---|
| 1 | 0.984976 | 282.519 | 0.050127 |
| 2 | 0.996400 | 229.964 | 0.226824 |
| 3 | 0.997757 | 115.951 | 0.610155 |
| 4 | 0.999427 | 98.285 | 0.669550 |
| 5 | 0.999722 | 57.994 | 0.805015 |
| 6 | 0.999853 | 53.097 | 0.821480 |
| 7 | 0.999963 | 52.010 | 0.825133 |
| 8 | 0.999976 | 48.842 | 0.835784 |
| 9 | 0.999982 | 34.344 | 0.884529 |
| 10 | 0.999986 | 31.050 | 0.895604 |
使用 湿度 模型对新观测值的预测响应
| 行 | 拟合值 | 拟合值标准误 | 95% 置信区间 | 95% 预测区间 |
|---|---|---|---|---|
| 1 | 14.5184 | 0.388841 | (13.7343, 15.3026) | (12.5910, 16.4459) |
| 2 | 9.3049 | 0.372712 | (8.5532, 10.0565) | (7.3904, 11.2193) |
| 3 | 14.1790 | 0.504606 | (13.1614, 15.1966) | (12.1454, 16.2127) |
| 4 | 16.4477 | 0.559704 | (15.3189, 17.5764) | (14.3562, 18.5391) |
| 5 | 15.1872 | 0.358044 | (14.4652, 15.9093) | (13.2842, 17.0903) |
| 6 | 9.4639 | 0.485613 | (8.4846, 10.4433) | (7.4492, 11.4787) |
使用 脂肪 模型对新观测值的预测响应
| 行 | 拟合值 | 拟合值标准误 | 95% 置信区间 | 95% 预测区间 |
|---|---|---|---|---|
| 1 | 18.7372 | 0.378459 | (17.9740, 19.5004) | (16.8612, 20.6132) |
| 2 | 15.3782 | 0.362762 | (14.6466, 16.1098) | (13.5149, 17.2415) |
| 3 | 20.7838 | 0.491134 | (19.7933, 21.7743) | (18.8044, 22.7632) |
| 4 | 14.3684 | 0.544761 | (13.2698, 15.4670) | (12.3328, 16.4040) |
| 5 | 16.6016 | 0.348485 | (15.8988, 17.3044) | (14.7494, 18.4538) |
| 6 | 20.7471 | 0.472648 | (19.7939, 21.7003) | (18.7861, 22.7080) |