带拟合线的图
带拟合线的图显示响应变量和预测变量数据。该图包含可表示正交回归方程的正交回归线。
您还可以选择在该图上显示用于比较的最小二乘拟合线。两条线之间较大的差距显示结果对您能否解释预测变量值的不确定性的依赖程度。最小二乘值等于正交回归的预测值,因此您还可以使用最小二乘线检查预测值。
解释
- 样本包含所有预测变量的整个范围内的数量足够的观察值。
- 样本不包含任何模型无法拟合的弯曲。
- 样本不包含可能对结果产生较强影响的异常值。尝试确定导致任何异常值的原因。更正任何数据输入错误或可识别的测量误差。考虑删除与异常的单次事件(也称为特殊原因)相关联的数据值。然后,重新执行分析。
您通常将正交回归用于临床化学或实验室,以确定两种工具或方法能否提供相似的测量值。
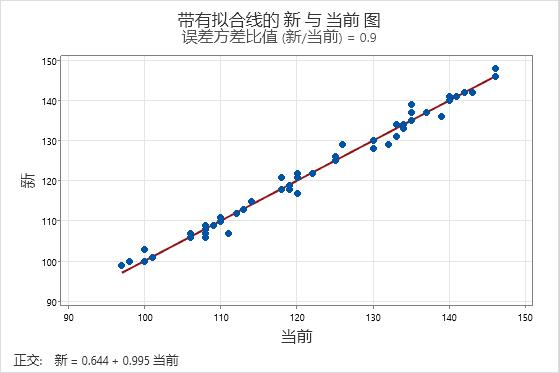
该图显示一个测量值示例,这些测量值来自两个可比较的仪器或方法。点服从具有最小散布的拟合线,该拟合线中不存在用来显示方法之间系统差值的模式。
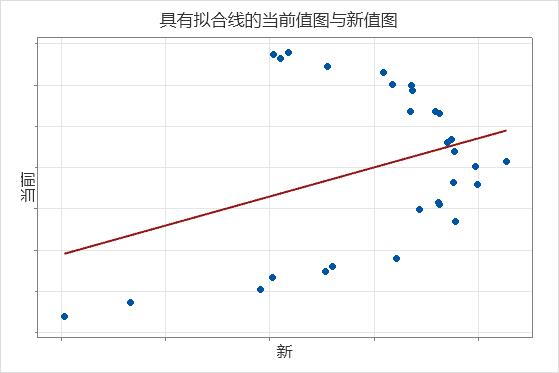
在下面的结果中,系数的置信区间不提供证据来说明两个仪器的测量值不同。但是,该图显示点紧密分布在拟合线附近,这表明两个仪器的测量值不可比较。由于数据与方程不拟合,因此通常的结论是仪器不同。
系数
| 预测变量 | 系数 | 系数标准误 | Z | P | 近似 95% 置信区间 |
|---|---|---|---|---|---|
| 常量 | -0.00000 | 0.215424 | -0.0000 | 1.000 | (-0.422224, 0.42222) |
| 新 | 1.00000 | 0.517586 | 1.9320 | 0.053 | (-0.014450, 2.01445) |
残差的直方图
残差的直方图显示所有观测值的残差分布。
解释
| 形式 | 模式的含义 |
|---|---|
| 朝着一个方向的长尾 | 偏度 |
| 远离其他条形的条形 | 异常值 |
您通常将正交回归用于临床化学或实验室,以确定两种工具或方法能否度量相同的事件。如果模型无法满足假设,有一种解释是这些方法无法度量相同的事件。
由于直方图的外观取决于用来对数据分组的区间数,因此在评估残差的正态性时不要使用直方图,而是改用正态概率图。
在具有大约 20 个或更多个数据点时,直方图效果最明显。则直方图上的每个条形无法包含足够的数据点,因而无法可靠地显示偏度或异常值。
残差的正态概率图
残差的正态概率图显示,当分布呈正态时,残差与期望值的关系。
解释
使用残差正态概率图可验证残差呈正态分布的假设。残差的正态概率图应该大致为一条直线。
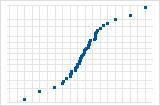
S 曲线表示长尾分布。
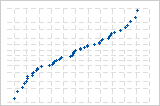
反向 S 曲线表示短尾分布。
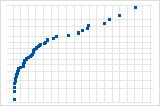
向下的曲线表示右偏斜分布。
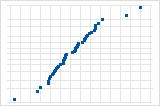
远离线的几个点表示分布中有异常值。
您通常将正交回归用于临床化学或实验室,以确定两种工具或方法能否度量相同的事件。如果您发现非正态模式,有一种解释是这些方法无法度量相同的事件。此外,可使用该模型检查其他残差图是否存在其他问题。如果残差不遵循正态分布,则置信区间和 P 值可能不准确。
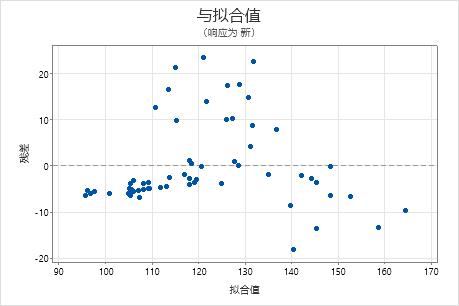
残差与拟合值
残差与拟合值图在 Y 轴上标绘残差,在 X 轴上标绘预测变量的拟合值。
您通常将正交回归用于临床化学或实验室,以确定两种工具或方法能否度量相同的事件。如果模型无法满足假设,有一种解释是这些方法无法度量相同的事件。
解释
使用残差与拟合值图可验证残差随机分布和具有常量方差的假设。理想情况下,点应当在 0 的两端随机分布,点中无可辨识的模式。
| 模式 | 模式的含义 |
|---|---|
| 残差相对拟合值呈扇形或不均匀分散 | 异方差 |
| 曲线 | 缺少高阶项 |
| 远离 0 的点 | 异常值 |
| 在 X 方向远离其他点的点 | 有影响的点 |

含异常值的图
其中一个点比所有其他点大得多。因此,该点是异常值。如果异常值过多,则模型可能不可接受。您应该尝试找出导致任何异常值的原因。更正任何数据输入错误或测量误差。考虑删除与异常的单次事件(也称为特殊原因)相关联的数据值。然后,重新执行分析。
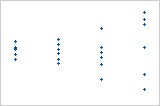
含异方差的图
残差的方差随拟合值增加。请注意,随着拟合值增大,残差之间的散布变宽。此模式表示残差的方差不相等(非恒定)。
残差与顺序
残差与顺序图按照数据的收集顺序显示残差。
解释
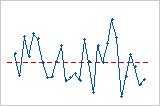
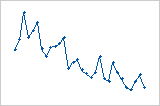
趋势
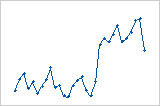
偏移
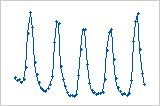
周期
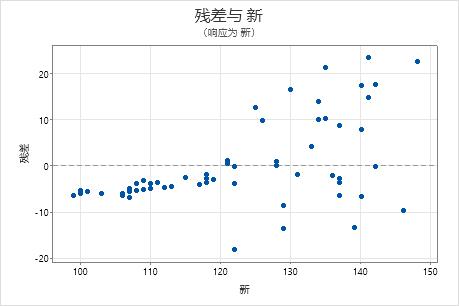
残差与变量
残差与变量的关系图显示残差与另一个变量的关系。已在模型中包含此变量。或者,模型中未包含此变量,但是猜测它会影响响应。
解释
您通常将正交回归用于临床化学或实验室,以确定两种工具或方法能否度量相同的事件。与响应变量或预测变量相关的残差图模式可以阐明两种方法的不同之处。
在这些结果中,残差与拟合值图显示所有高残差值均位于该图中间的模式。残差与响应变量图表明当新方法的读数变大时,另一种方法的一致性就会变差。