例如,一家医疗设备公司的工程师想确定该公司的新型血压监视器是否与其他公司生产的类似监视器等效。工程师使用两台血压监视器分别测量由 60 人组成的随机样本的心脏收缩血压。
为了确定两台监视器是否等效,工程师采用正交回归。在收集数据以进行正交回归之前,工程师对每台监视器单独进行研究以估计方差。新监视器的方差为 1.08。另一家公司的监视器的方差为 1.2。工程师决定为新监视器赋予响应变量,为另一家公司的监视器赋予预测变量。使用这些赋值后,误差的方差比为 1.08 / 1.2 = 0.9。
注意
如果工程师决定交换赋值,则误差的方差比将为 1.2 / 1.08 = 1.1111。
- 打开样本数据 血压.MWX。
- 选择。
- 在响应 (Y)中,输入新。
- 在预测变量 (X)中,输入当前。
- 在误差方差比值 (Y/X)中,输入 0.90。
- 单击确定。
解释结果
如果以下任一条件成立,则结果中将提供血压监测仪不等效的证据:
- 斜率的置信区间不包含 1。
- 常量的置信区间不包含 0。
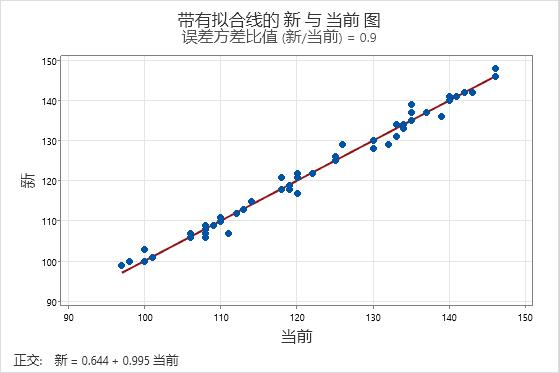
误差方差比值 (新/当前): 0.9
回归方程
新 = 0.644 + 0.995 当前
新 = 0.644 + 0.995 当前
系数
| 预测变量 | 系数 | 系数标准误 | Z | P | 近似 95% 置信区间 |
|---|---|---|---|---|---|
| 常量 | 0.64441 | 1.74470 | 0.3694 | 0.712 | (-2.77513, 4.06395) |
| 当前 | 0.99542 | 0.01415 | 70.3461 | 0.000 | (0.96769, 1.02315) |
误差方差
| 变量 | 方差 |
|---|---|
| 新 | 1.07856 |
| 当前 | 1.19840 |