请选择您所选的方法或公式。
拟合值
第 n 个观测值在 θ* 处的预期响应:


表示法
| 项 | 说明 |
|---|---|
| θ* | 最后一次迭代 |
| xn | 预测变量在第 n 个观测值处的值向量 |
| v0 | 梯度矩阵 = ( ∂f(xn, θ) / ∂θp ),即 f(x0, θ) 的偏导数的 P*1 向量在 θ* 处的求值 |
预测的置信区间
在指定的预测变量设置条件下,均值响应将落入的范围。预测的近似 100(1 - α)% 置信区间为:
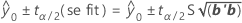
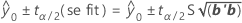
表示法
| 项 | 说明 |
|---|---|
| tα/2 | 自由度为 N – P 的 t 分布的 α/2 上限点 |
| se fit | 拟合值的标准误 |
| n | 第 n 个观测值 |
| N | 观测值总数 |
| P | 自由(解锁)参数个数 |
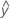 | 拟合值 |
| b | (R')-1v0 |
| R | 最后一次迭代的 Vi 的 QR 分解中的(上三角部分)R 矩阵 |
| v0 | 梯度矩阵 = ( ∂f(xn, θ) / ∂θp),Pf(x0, θ) 的偏导数的 P*1 向量在 θ* 处的求值 |
| S |
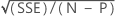 |
预测区间
一个新观测值的预测响应将落入的极差。新观测值的近似 100(1 - α)% 预测区间为:
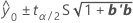
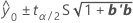
表示法
| 项 | 说明 |
|---|---|
| tα/2 | 自由度为 N – P 的 t 分布的 α/2 上限点 |
| se fit | 拟合值的标准误 |
| n | 第 n 个观测值 |
| N | 观测值总数 |
| P | 自由(解锁)参数的个数 |
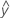 | 拟合值 |
| b | (R')-1v0 |
| R | 最后一次迭代的 Vi 的 QR 分解中的(上三角部分)R 矩阵 |
| v0 | 梯梯度矩阵 = ( ∂f(xn, θ) / ∂θp),即 f(x0, θ) 的偏导数的 P*1 向量在 θ* 处的求值 |
| S |
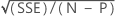 |
拟合值的标准误
拟合值的近似标准误为:






表示法
| 项 | 说明 |
|---|---|
| n | 第 n 个观测值 |
| N | 观测值总数 |
| P | 自由(解锁)参数的个数 |
| x0 | 预测变量值的向量 |
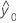 | f(x0, θ*) |
| v0 | 梯度矩阵 = ( ∂f(xn, θ) / ∂θp),即 f(x0, θ) 的偏导数的 P*1 向量在 θ* 处的求值 |
| S |
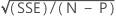 |
