请选择您所选的方法或公式。
参数约束
通过变换参数强制执行参数约束。1
| 如果 | 得到 |
|---|---|
| a < θ | θ = a + exp( φ ) |
| θ < b | θ = b - exp( φ ) |
| a < θ < b | θ = a +((b - a) / (1 + exp( -φ ))) |
| 项 | 说明 |
|---|---|
| a 和 b | 数字常量 |
| θ's | 参数 |
| φ | 变换的参数 |
Minitab 会执行这些变换并显示基于原始参数的结果。
- Bates 和 Watts (1988)。Nonlinear Regression Analysis and Its Applications(非线性回归分析及其应用)。John Wiley & Sons, Inc.
参数估计的标准误
θp 估计值的近似标准误等于 S 乘以 的对角线元素 p 的平方根 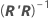 ,书写方式如下:
,书写方式如下:

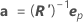

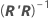 ,书写方式如下:
,书写方式如下:

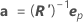

表示法
| 项 | 说明 |
|---|---|
| n | 第 n 个观测值 |
| N | 观测值总数 |
| p | 自由(解锁)参数的个数 |
| R | 最后一次迭代的 Vi 的 QR 分解中的(上三角部分)R 矩阵 |
| V0 | 梯度矩阵 = ( ∂f(xn, θ) / ∂θp),即 f(x0, θ) 的偏导数的 P*1 向量在 θ* 处的求值 |
| S |
 |
参数估计的相关矩阵
参数估计的近似方差-协方差矩阵为:
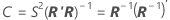
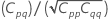

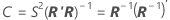
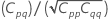

表示法
| 项 | 说明 |
|---|---|
| R | 最后一次迭代的 Vi 的 QR 分解中的(上三角部分)R 矩阵 |
| P | 自由(解锁)参数的个数 |
| v0 | 梯度矩阵 = ( ∂f(xn, θ) / ∂θ p),即 f( x0, θ) 的偏导数的 P*1 向量在 θ* 处的求值 |
| θ's | 参数 |
参数的剖面似然置信区间
让具有 θ* 的 θ = (θ1, . . . . θp) * 为 θ 的最后一次迭代。
基于似然的 100 (1 - α) % 置信限满足:
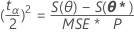
其中,S( θp ) 是在保持 θp 不变和最小化其他参数时获得的 SSE。1 这相当于以下求解过程:
S(θp) = S(θ*) + (tα/2)2 MSE
表示法
| 项 | 说明 |
|---|---|
| θ's | 参数 |
| n | 第 n 个观测值 |
| N | 观测值总数 |
| P | 自由(解锁)参数的个数 |
| tα/2 | 自由度为 N - P 的 t 分布的 α/2 上限点 |
| S(θ) | 误差平方和 |
| MSE | 均方误 |
- Bates 和 Watts (1988)。Nonlinear Regression Analysis and Its Applications(非线性回归分析及其应用)。John Wiley & Sons, Inc.
