请选择您所选的方法或公式。
表示法
观测值 n 的预期函数可表示为:
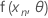
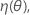
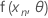 。
。

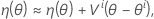
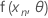
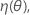
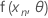 。
。
η 的 Jacobian 是 N X P 矩阵,其元素等于预期函数相对于参数的偏导数:

然后,η 的线性近似为:
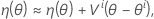
让 θ* 表示最小二乘估计值。
Gauss-Newton
默认情况下,Minitab 会使用 Gauss-Newton 法确定最小二乘估计值。该方法使用预期函数的线性近似逐步改进 θ 的初始猜测 θ0,随后该方法将不断改进估计值,直到相对偏移落在规定公差1 下方。也就是说,Minitab 会将有关 θ0 的一阶泰勒级数预期函数 f(xn,θ) 展开为:
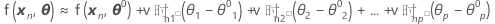
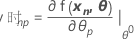
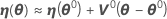

 并且
并且
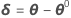


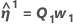
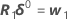 .
.

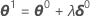
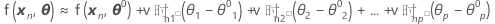
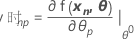
包括所有 N 个案例
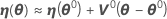

其中

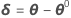
Minitab 会计算 Gauss 增量 δ0 以最小化近似残差平方和 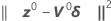 ,使用:
,使用:


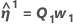
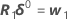 .
.
点

现在应该比 η(θ0) 更靠近 y,Minitab 会使用值 θ1 = θ0 + δ0 执行其他迭代,方法是计算新残差 z1 = y - η(θ1)、一个新迭代矩阵 V1 和一个新增量。Minitab 会在收敛前重复执行此过程,这出现在因增量太小而导致参数向量元素中的变化毫无用处时。
有时,Gauss-Newton 增量会使平方和增大。出现此情况时,线性近似仍然是对 η(θ0) 周围足够小的区域的实际面积的相近的估算。为降低平方和,Minitab 会引入步长因子 λ,然后计算:
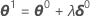
- Bates 和 Watts (1988)。Nonlinear Regression Analysis and Its Applications(非线性回归分析及其应用)。John Wiley & Sons, Inc.
Levenberg-Marquardt
当梯度矩阵 V 中的列共线时,该矩阵可能会变为奇异阵,从而导致 Gauss-Newton 迭代的不规律性。为处理奇异阵,Minitab 可以将 Gauss-Newton 增量修改为 Levenberg 折衷值:
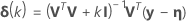
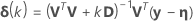
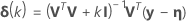
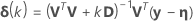
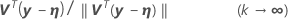 .1
.1
- Bates 和 Watts (1988)。Nonlinear Regression Analysis and Its Applications(非线性回归分析及其应用)。John Wiley & Sons, Inc.
相对偏移收敛标准
默认情况下,当相对偏移小于 1.0e-5 时,Minitab 声明收敛。这可以确保任何推断都不会受如下情况的重大影响:当前参数向量小于置信圆盘区域半径(根据最小二乘点计算得出)的 0.001%。1
1. Bates 和 Watts (1988)。Nonlinear Regression Analysis and Its Applications(非线性回归分析及其应用)。John Wiley & Sons, Inc.
