请查找定义和解释指导,了解每个残差图。
残差的直方图
残差的直方图显示所有观测值的残差分布。
解释
使用残差的直方图可确定数据是偏斜还是包含异常值。下列表中的模式可能表明模型不符合模型假定。
| 模式 | 模式的含义 |
|---|---|
| 一个方向的长尾 | 偏度 |
| 远离其他条形的条形 | 异常值 |
因为直方图的外观取决于用来进行数据分组的区间数,所以请勿使用直方图评估残差的正态性。反之,可使用正态概率图。
在具有大约 20 个或更多个数据点时,直方图效果最明显。如果样本过小,则直方图的每个条形未包含可靠显示偏度或异常值的足够数据点。
残差的正态概率图
残差的正态概率图显示,当分布呈正态时,残差与期望值的关系。
解释
使用残差正态概率图可验证残差呈正态分布的假设。残差的正态概率图应该大致为一条直线。
以下模式违反了残差呈正态分布这一假设。
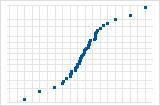

S 曲线表示长尾分布。

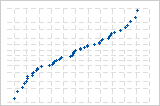
反向 S 曲线表示短尾分布。

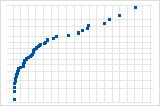
向下的曲线表示右偏斜分布。

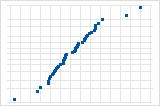
远离线的几个点表示分布中有异常值。
如果遇到非正态模式,请使用其他残差图检查模型的其他问题,例如,缺失项或时序效应。如果残差未遵循正态分布,则置信区间和 p 值可能不正确。
残差与拟合值
残差与拟合值图形分别在 y 轴和 x 轴上绘制残差和拟合值。
解释
使用残差与拟合值图可验证残差随机分布和具有常量方差的假设。理想情况下,点应当在 0 的两端随机分布,点中无可辨识的模式。
下表中的模式可能表示该模型不满足模型假设。
| 模式 | 模式的含义 |
|---|---|
| 残差相对拟合值呈扇形或不均匀分散 | 异方差 |
| 曲线 | 缺少高阶项 |
| 远离 0 的点 | 异常值 |
| 在 X 方向远离其他点的点 | 有影响的点 |
下图显示了残差方差为常量这一假设中的异常值和冲突。

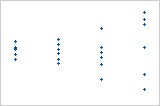

含异常值的图
其中一个点比所有其他点大得多。因此,该点是异常值。如果异常值过多,则模型可能不可接受。您应该尝试找出导致任何异常值的原因。更正任何数据输入错误或测量误差。考虑删除与异常的单次事件(也称为特殊原因)相关联的数据值。然后,重新执行分析。
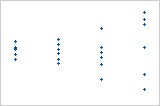
含异方差的图
残差的方差随拟合值增加。请注意,随着拟合值增大,残差之间的散布变宽。此模式表示残差的方差不相等(非恒定)。
残差与顺序
残差与顺序图按照数据的收集顺序显示残差。
解释
使用残差与顺序图可验证残差独立于其他残差的假设。当以时序显示时,独立残差不显示趋势或模式。点中的模式可能表明,彼此相近的残差可能相关联,因此并不独立。理想情况下,图中的残差应围绕中心线随机分布: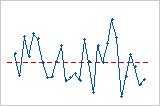

如果查看模式,便可查出原因。下列类型的模式可能表明残差属于依赖项。
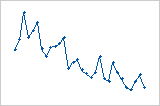
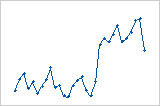
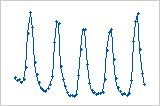

趋势

偏移

周期
残差与变量
残差与变量的关系图显示残差与另一个变量的关系。已在模型中包含此变量。或者,模型中未包含此变量,但是猜测它会影响响应。
解释
如果在残差中看到非随机图形,则表明变量会系统性地影响响应。请考虑在分析中包含此变量。
