例如,NIST(美国国家标准与技术研究院)的研究人员希望了解铜的热膨胀系数与开尔文温度之间的关系。
先前研究表明,具有 7 个参数的非线性模型提供了充分拟合。研究人员使用非线性回归估计模型中的参数。
- 打开样本数据 铜膨胀.MWX。
- 选择。
- 在响应中,输入膨胀系数。
- 在直接编辑中,复制并粘贴或键入以下值:(b1+b2*开尔文温度+b3*开尔文温度^2+b4*开尔文温度^3)/(1+b5*开尔文温度+b6*开尔文温度^2+b7*开尔文温度^3)
- 单击参数。
- 在必需的初始值中,输入以下值:
参数 值 b1 1 b2 -0.1 b3 0.005 b4 -1e-6 b5 -0.005 b6 0.001 b7 -1e-7 - 单击每个对话框中的确定。
解释结果
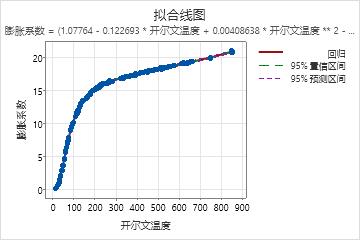
拟合值图显示拟合线沿观测值分布,这直观地表明模型与数据拟合。失拟检验的 P 值为 0.679,这就没有证据表明模型对数据的拟合效果很差。
关于高度相关参数的警告表明,至少有一对参数相关性的绝对值大于 0.99。但是,由于先前的研究表明,具有 7 个参数的非线性模型提供充分的数据拟合,因此研究人员不更改模型。
方法
| 算法 | Gauss-Newton |
|---|---|
| 最大迭代次数 | 200 |
| 公差 | 0.00001 |
参数的起始值
| 参数 | 值 |
|---|---|
| b1 | 1 |
| b2 | -0.1 |
| b3 | 0.005 |
| b4 | -0.000001 |
| b5 | -0.005 |
| b6 | 0.001 |
| b7 | -0.0000001 |
方程
膨胀系数 = (1.07764 - 0.122693 * 开尔文温度 + 0.00408638 * 开尔文温度 ** 2 - 1.42627E-06 * 开尔文温度 ** 3) / (1
- 0.00576099 * 开尔文温度 + 0.000240537 * 开尔文温度 ** 2 - 1.23144E-07 * 开尔文温度 ** 3)
- 0.00576099 * 开尔文温度 + 0.000240537 * 开尔文温度 ** 2 - 1.23144E-07 * 开尔文温度 ** 3)
参数估计
| 参数 | 估计 | 标准误估计值 |
|---|---|---|
| b1 | 1.07764 | 0.170702 |
| b2 | -0.12269 | 0.012000 |
| b3 | 0.00409 | 0.000225 |
| b4 | -0.00000 | 0.000000 |
| b5 | -0.00576 | 0.000247 |
| b6 | 0.00024 | 0.000010 |
| b7 | -0.00000 | 0.000000 |
失拟
| 来源 | 自由度 | SS | MS | F | P |
|---|---|---|---|---|---|
| 误差 | 229 | 1.53244 | 0.0066919 | ||
| 失拟 | 228 | 1.52583 | 0.0066922 | 1.01 | 0.679 |
| 纯误差 | 1 | 0.00661 | 0.0066125 |
汇总
| 迭代 | 15 |
|---|---|
| 最终 SSE | 1.53244 |
| DFE | 229 |
| MSE | 0.0066919 |
| S | 0.0818039 |
