步骤 1:确定响应和项之间的关联在统计意义上是否显著
- P 值 ≤ α:关联在统计意义上显著
- 如果 P 值小于或等于显著性水平,则可以得出响应变量与项之间的关联在统计意义上显著的结论。如果您拟合二次模型或立方模型,而且二次项或立方项为显著,则可以得出数据包含弯曲的结论。
- P 值 > α:关联在统计意义上不显著
-
如果 p 值大于显著性水平,则无法得出响应变量与该项之间的关联在统计意义上显著的结论。如果您拟合二次模型或立方模型,而二次项或立方项在统计意义上不显著,则可能需要选择其他模型。
方差分析
| 来源 | 自由度 | SS | MS | F | P |
|---|---|---|---|---|---|
| 回归 | 2 | 12189.4 | 6094.70 | 106.54 | 0.000 |
| 误差 | 26 | 1487.3 | 57.21 | ||
| 合计 | 28 | 13676.7 |
方差的序贯分析
| 来源 | 自由度 | SS | F | P |
|---|---|---|---|---|
| 线性 | 1 | 11552.8 | 146.86 | 0.000 |
| 二次 | 1 | 636.6 | 11.13 | 0.003 |
关键结果:P 值
在这些结果中,线性项密度的 p 值为 0.000,二次项密度2 的 p 值为 0.003。这两个 p 值都小于显著性水平 0.05。这些结果表示硬度和密度之间的关联在统计上显著。
步骤 2:确定回归线是否与数据拟合
- 在具有所有预测变量值的整个范围中,样本包含充足的观测值个数。
- 模型与数据中的任何弯曲正确拟合。如果要拟合线性模型并查看数据中的弯曲,则重复执行分析并选择二次模型或立方模型。要确定最佳模型,请检查图及拟合优度统计量。查看模型中项的 p 值,以确保这些项统计意义显著,并应用流程知识来评估实际显著性。
- 查找任何异常值,这些值可能对结果产生较强的影响。尝试确定导致任何异常值的原因。更正任何数据输入错误或测量误差。考虑删除与异常的单次事件(也称为特殊原因)相关联的数据值。然后,重新执行分析。有关检测异常值的详细信息,请转到异常观测值。
步骤 3:检查项如何与响应关联
如果项的 P 值显著,则可以检查回归方程和系数以了解项如何与响应关联。
使用回归方程可描述模型中响应和项之间的关系。回归方程是回归线的代数表示。线性模型的回归方程采取如下形式:Y= b0 + b1x1。在回归方程中,Y 是响应变量,b0 是常量或截距,b1 是线性项的估计系数(也称为直线斜率),x1 是项值。
项系数表示该项中单位变化对应的均值响应变化。系数的符号表明项与响应之间关系的方向。如果系数为负,随着项递增,响应的均值会递减。如果系数为正,随着项数递增,响应的均值也会递增。
例如,某经理要确定员工在工作技能检验中的分数是否可以使用回归模型 y = 130 + 4.3x 进行预测。在方程中,x 是内部培训的小时数(0 到 20 之间),而 y 是检验分数。系数或斜率为 4.3,这表示每小时培训的平均检验分数按照 4.3 点递增。
有关系数的详细信息,请转到回归系数。
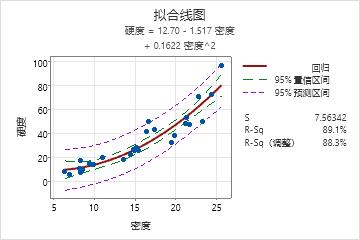
硬度 = 12.70 - 1.517 密度 + 0.1622 密度^2
模型汇总
| S | R-sq | R-sq(调整) |
|---|---|---|
| 7.56342 | 89.13% | 88.29% |
关键结果:回归方程、系数
预测变量密度的系数为 –1.517,密度2 的系数为 0.1622。因此,对于二次关系,密度值越大,刨花板平均硬度增加的速度越快。
步骤 4:确定模型与数据的拟合优度
要确定模型与数据的拟合优度,请检查模型汇总表中的拟合优度统计量。
- R-sq
-
R2 是由模型解释的响应的变异百分比。R2 值越高,模型与数据的拟合度越好。R2 始终介于 0% 和 100% 之间。
如果向模型添加其他预测变量,则 R2 会始终增加。例如,最佳的五预测变量模型的 R2 始终比最佳的四预测变量模型的高。因此,比较相同大小的模型时 R2 最有效。
- R-sq(调整)
-
在想要比较具有不同数量的预测变量的情况下,使用调整的 R2。如果向模型添加预测变量,即使模型没有实际改善,R2 也会始终增加。调整的 R2 值包含模型中的预测变量数,以便帮助您选择正确的模型。
-
样本数量较小则不能提供对于响应变量和预测变量之间关系强度的精确估计。如果需要 R2 更为精确,则应当使用较大的样本(通常为 40 或更多)。
-
拟合优度统计量只是模型拟合数据优度的一种度量。即使模型具有合意的值,您也应当检查残差图,以验证模型是否符合模型假设。
硬度 = 12.70 - 1.517 密度 + 0.1622 密度^2
模型汇总
| S | R-sq | R-sq(调整) |
|---|---|---|
| 7.56342 | 89.13% | 88.29% |
关键结果:R-sq
在这些结果中,刨花板密度大约可以解释刨花板硬度中 89% 的变异。R2 值表示模型可以很好地拟合数据。
步骤 5:确定模型是否符合分析的假设
使用残差图可帮助您确定模型是否适用并符合分析的假设。如果不符合此假设,则模型可能无法充分拟合数据,在解释结果时应当格外小心。
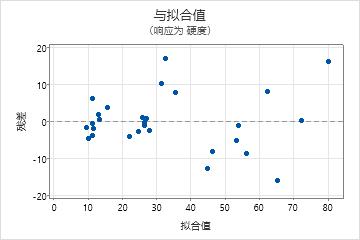
残差与拟合值图
使用残差与拟合值图可验证残差随机分布且具有恒定方差的假设的假设。理想情况下,点应当在 0 的两端随机分布,点中无可辨识的模式。
| 模式 | 模式可能指示的内容 |
|---|---|
| 残差相对拟合值呈扇形或不均匀分散 | 异方差 |
| 曲线 | 缺少高阶项 |
| 远离 0 的点 | 异常值 |
| 在 X 方向远离其他点的点 | 有影响的点 |
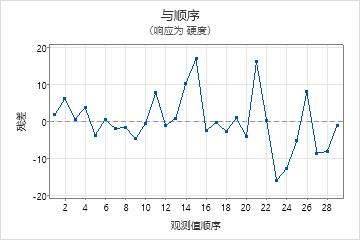
残差与顺序图
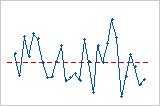
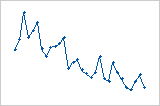
趋势
班次
周期
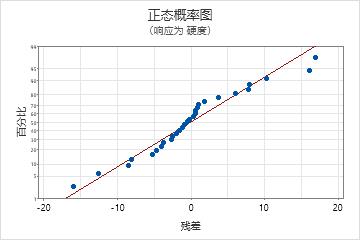
正态概率图
使用残差的正态概率图可验证残差呈正态分布的假设。残差的正态概率图应该大致为一条直线。
| 模式 | 模式可能指示的内容 |
|---|---|
| 非直线 | 非正态性 |
| 远离直线的点 | 异常值 |
| 斜率不断变化 | 未确定的变量 |
有关如何处理残差图模式的详细信息,请转到拟合线图的残差图。
