请选择您所选的方法或公式。
系数 (Coef)
简单线性回归中系数或斜率的公式为:
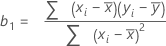
截距 (b0) 的公式为:

在矩阵项中,计算多个回归中的系数的向量的公式为:
b = (X'X)-1X'y
表示法
| 项 | 说明 |
|---|---|
| yi | 观测的第 i 个响应值 |
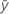 | 平均值响应变量 |
| xi | 第 i 个预测变量值 |
 | 平均值预测变量 |
| X | 设计矩阵 |
| y | 响应矩阵 |
系数的标准误(系数标准误)
对于简单线性回归,系数的标准误为:
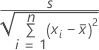
多个回归的系数标准误都是此矩阵的对角线元素的平方根:
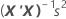
表示法
| 项 | 说明 |
|---|---|
| xi | 第 i 个预测变量值 |
 | 预测变量的平均值 |
| X | 设计矩阵 |
| X' | 设计矩阵的转置 |
| s2 | 均方误 |
T 值
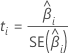
表示法
| 项 | 说明 |
|---|---|
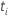 | 检验统计量(对于第  系数) 系数) |
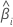 | 第 估计系数 估计系数 |
 | 标准误(对于第 估计系数 估计系数 |
P 值 – 系数表
回归系数等于 0 的原假设的双面 p 值为:
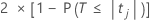
自由度是误差的自由度,如下所示:
n – p – 1
表示法
| 项 | 说明 |
|---|---|
 | t 分布的累积分布函数具有等于误差自由度的自由度。 |
| tj | 第 j 个系数的 t 统计量。 |
| n | 数据集中的观测值个数。 |
| p | 项的自由度总和。项不包含常量。 |
