残差的直方图
残差的直方图显示所有观测值的残差分布。
解释
| 模式 | 模式的含义 |
|---|---|
| 一个方向的长尾 | 偏度 |
| 远离其他条形的条形 | 异常值 |
因为直方图的外观取决于用来进行数据分组的区间数,所以请勿使用直方图评估残差的正态性。反之,可使用正态概率图。
在具有大约 20 个或更多个数据点时,直方图效果最明显。如果样本过小,则直方图的每个条形未包含可靠显示偏度或异常值的足够数据点。
残差的正态概率图
残差的正态概率图显示,当分布呈正态时,残差与期望值的关系。
解释
使用残差正态概率图可验证残差呈正态分布的假设。残差的正态概率图应该大致为一条直线。
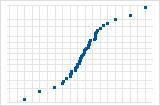
S 曲线表示长尾分布。
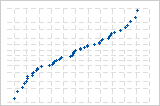
反向 S 曲线表示短尾分布。
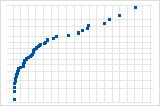
向下的曲线表示右偏斜分布。
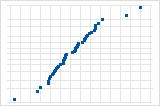
远离线的几个点表示分布中有异常值。
如果遇到非正态模式,请使用其他残差图检查模型的其他问题,例如,缺失项或时序效应。如果残差未遵循正态分布,则置信区间和 p 值可能不正确。
残差与拟合值
残差与拟合值图形分别在 y 轴和 x 轴上绘制残差和拟合值。
解释
使用残差与拟合值图可验证残差随机分布且具有恒定方差的假设的假设。理想情况下,点应当在 0 的两端随机分布,点中无可辨识的模式。
| 模式 | 模式可能指示的内容 |
|---|---|
| 残差相对拟合值呈扇形或不均匀分散 | 异方差 |
| 曲线 | 缺少高阶项 |
| 远离 0 的点 | 异常值 |
| 在 X 方向远离其他点的点 | 有影响的点 |

含异常值的图
其中一个点比所有其他点大得多。因此,该点是异常值。如果异常值过多,则模型可能不可接受。您应该尝试找出导致任何异常值的原因。更正任何数据输入错误或测量误差。考虑删除与异常的单次事件(也称为特殊原因)相关联的数据值。然后,重新执行分析。
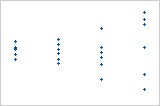
含异方差的图
残差的方差随拟合值增加。请注意,随着拟合值增大,残差之间的散布变宽。此模式表示残差的方差不相等(非恒定)。
要确定残差与拟合值图中的任何模式或异常值,请考虑以下解决方案:
| 问题 | 可能解决方案 |
|---|---|
| 异方差 | 考虑使用具有 Box-Cox 变换或权重的拟合回归模型。 |
| 异常值或有影响的点 |
|
残差与顺序
残差与顺序图按照数据的收集顺序显示残差。
解释
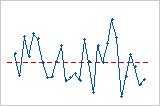
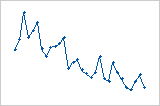
趋势
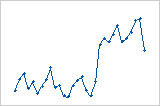
偏移
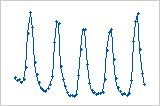
周期
残差与变量
残差与变量的关系图显示残差与另一个变量的关系。已在模型中包含此变量。或者,模型中未包含此变量,但是猜测它会影响响应。
解释
如果在残差中看到非随机图形,则表明变量会系统性地影响响应。请考虑在分析中包含此变量。
检验数据集的残差图
解释
由于训练和检验数据集通常来自同一总体,因此您希望在每个数据集的残差图中看到相同的模式。残差图的不同模式可能表明训练数据集和检验数据集中的观测值之间存在系统差异。
尽管模式通常相同,但检验数据集的残差图可能与训练数据集的残差图略有不同。例如,由于检验数据集不在模型拟合过程中,残差的平均值可能为非零。
