研究化学家想要了解多个预测变量与棉布抗皱性的关联性。化学家检查 32 件在不同的凝固时间、凝固温度、甲醛浓度和催化剂比率下生产出的棉纤维素。对每件棉布都记录了耐压等级(用来度量抗皱性)。
The chemist performs a multiple regression analysis to fit a model with the predictors and eliminate the predictors that do not have a statistically significant relationship with the response.
- 打开样本数据抗皱性.MWX.
- 选择。
- 在响应中,输入评级。
- 在连续预测变量中,输入浓度比率温度时间。
- 单击图形。
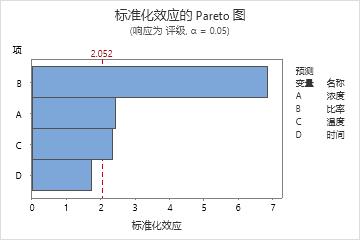
- 在效应图下,选择Pareto。
- 在残差图下,选择四合一。
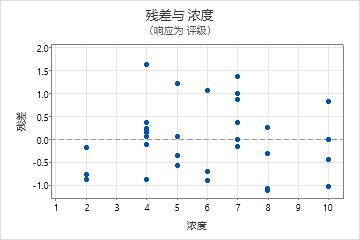
- 在残差与变量中,输入浓度比率温度时间。
- 单击每个对话框中的确定。
解释结果
作为预测变量的温度、催化剂比率和甲醛浓度的 p 值小于显著水平 0.05。这些结果表示这些预测变量对抗皱性具有统计意义上非常显著的效应。时间的 p 值大于 0.05,这表示没有足够的证据可以断定时间与响应相关。化学家可能需要重新拟合不具有此预测变量的模型。
Pareto 图显示在显著性水平为 0.05 时,温度、催化剂比率和甲醛浓度的效应在统计意义上显著。最大的效应是催化剂比率,因为它延伸得最远。最小的效应是时间效应,因为它延伸得最近。
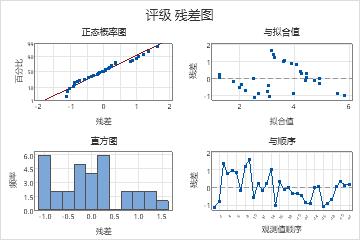
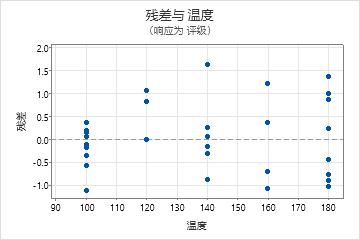
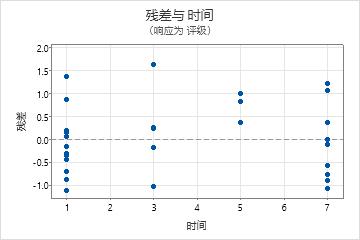
此残差图指示该模型可能有问题。
- 残差与拟合值图中的点并未随机分布在零附近。但似乎存在表示不同数据组的点群集。化学家应该研究这些组以确定其原因。
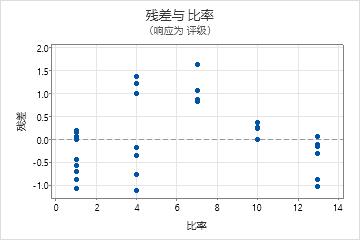
- 残差与比率图显示了弯曲,这表明催化剂比率与皱纹之间具有曲线关系。化学家应该考虑向该模型添加比率的二次项。
回归方程
| 评级 | = | -0.756 + 0.1545 浓度 + 0.2171 比率 + 0.01081 温度 + 0.0946 时间 |
|---|
系数
| 项 | 系数 | 系数标准误 | T 值 | P 值 | 方差膨胀因子 |
|---|---|---|---|---|---|
| 常量 | -0.756 | 0.736 | -1.03 | 0.314 | |
| 浓度 | 0.1545 | 0.0633 | 2.44 | 0.022 | 1.03 |
| 比率 | 0.2171 | 0.0316 | 6.86 | 0.000 | 1.02 |
| 温度 | 0.01081 | 0.00462 | 2.34 | 0.027 | 1.04 |
| 时间 | 0.0946 | 0.0546 | 1.73 | 0.094 | 1.00 |
模型汇总
| S | R-sq | R-sq(调整) | R-sq(预测) |
|---|---|---|---|
| 0.811840 | 72.92% | 68.90% | 62.81% |
方差分析
| 来源 | 自由度 | Adj SS | Adj MS | F 值 | P 值 |
|---|---|---|---|---|---|
| 回归 | 4 | 47.9096 | 11.9774 | 18.17 | 0.000 |
| 浓度 | 1 | 3.9232 | 3.9232 | 5.95 | 0.022 |
| 比率 | 1 | 31.0216 | 31.0216 | 47.07 | 0.000 |
| 温度 | 1 | 3.6031 | 3.6031 | 5.47 | 0.027 |
| 时间 | 1 | 1.9839 | 1.9839 | 3.01 | 0.094 |
| 误差 | 27 | 17.7953 | 0.6591 | ||
| 失拟 | 25 | 17.7836 | 0.7113 | 121.94 | 0.008 |
| 纯误差 | 2 | 0.0117 | 0.0058 | ||
| 合计 | 31 | 65.7049 |
异常观测值的拟合和诊断
| 观测值 | 评级 | 拟合值 | 残差 | 标准化残差 | |
|---|---|---|---|---|---|
| 9 | 4.800 | 3.178 | 1.622 | 2.06 | R |