拟合 Poisson 模型的模型汇总表格

在模型汇总表格中查找每个统计量的定义和解释指导。

关于本主题

偏差 R-Sq
偏差 R 平方（调整）
检验偏差 R 平方
K 折叠偏差 R 平方
AIC、AICc 和 BIC

偏差 R-Sq

偏差 R² 通常被视为由模型解释的响应变量中的总偏差的比率。

解释

偏差 R² 越高，模型拟合数据的优度越高。偏差 R² 始终在 0% 和 100%之间。

如果向模型添加其他项，则偏差 R² 会始终增加。例如，最佳的 5 项模型的 R² 始终比最佳的 4 项模型的高（至少一样高）。因此，比较相同大小的模型时，偏差 R² 最有用。

拟合优度统计量只是模型拟合数据优度的一种度量。即使模型具有合意的值，您也应当检查残差图和拟合优度检验，以评估模型拟合数据的优度。

您可以使用拟合线图演示不同的偏差 R² 值。第一张图演示的模型解释了响应变量中约 96% 的偏差。第二张图演示的模型解释了响应变量中约 60% 的偏差。模型解释的偏差越多，数据点坐落的位置越靠近曲线。从理论上讲，如果模型可以解释 100% 的偏差，则拟合值将始终等于观测值，并且所有数据点都将落于曲线上。

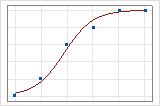
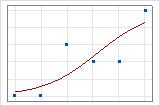
数据排列影响偏差 R² 值。每行多个试验的数据的偏差 R² 通常比每行单个试验的数据高。偏差 R² 值仅在使用相同数据格式的两个模型之间可比较。有关更多信息，请转到数据格式对二元 Logistic 回归中拟合优度的影响。

偏差 R 平方（调整）

调整的偏差 R² 是由模型解释的响应中偏差的比率，相对于观测值数，已调整了模型中的预测变量数。

解释

使用调整的偏差 R² 来比较具有不同项数的模型。如果向模型添加项，偏差 R² 也会始终增加。调整的偏差 R² 值在模型中包含了项数，以帮助您选择正确的模型。

例如，您效力于一家薯片公司，该公司正在检查影响碎薯片的因子。当您添加预测变量时，将得到以下结果：

步阶	马铃薯百分比	冷却速率	加工温度	偏差 R²	调整的偏差 R²
0	X			52%	51%
1	X	X		63%	62%
3	X	X	X	65%	62%

第一步产生在统计意义上显著的回归模型。第二步向模型中添加冷却速率，它会增加调整的方差 R²，这表明冷却速率会改善模型。第三部向模型中添加烹饪温度，它会增加方差 R²，但不会增加调整的方差 R²。这些结果表明，加工温度不会改善模型。基于这些结果，您可以考虑从模型中删除烹饪温度。

数据格式会影响调整的偏差 R² 值。对于相同的数据，每行多个试验的数据的调整偏差 R² 通常比每行单个试验的数据高。仅使用调整的偏差 R² 比较具有相同数据格式的模型的拟合。有关详细信息，请转到数据格式对二元 Logistic 回归中拟合优度的影响。

检验偏差 R 平方

检验偏差 R² 通常被视为模型解释的检验数据集响应变量中总偏差的比例。

解释

使用检验偏差 R² 确定模型与新数据的拟合度。具有较大检验偏差 R² 值的模型往往对新数据的表现更好。您可以使用检验偏差 R² 来比较不同模型的性能。

明显小于偏差 R² 的检验偏差 R² 可能表示模型过度拟合。当您为在总体中不重要的效应添加项时，将出现过度拟合模型。该模型变为根据训练数据定制的模型，因此对于预测总体数据可能没有帮助。

例如，一家金融咨询公司的分析师开发了一个模型，用于预测未来的市场状况。该模型看似很理想，因为它的 R² 为 87%。但是，检验偏差 R² 为 52%，这表明模型可能过度拟合。

高检验偏差 R² 值本身并不表示模型满足模型假设。您应该检查残差图以验证假设。

K 折叠偏差 R 平方

K 折叠偏差 R² 通常被视为模型解释的验证数据响应变量中总偏差的比率。

解释

使用 K 折叠偏差 R² 确定模型与新数据的拟合度。具有较大 K 折叠偏差 R² 值的模型往往对新数据的表现更好。您可以使用 K 折叠偏差 R² 值来比较不同模型的性能。

明显小于偏差 R² 的 K 折叠偏差 R² 可能表示模型过度拟合。当您为在总体中不重要的效应添加项时，将出现过度拟合模型。该模型变为根据训练数据集定制的模型，因此对于预测总体数据可能没有帮助。

例如，一家金融咨询公司的分析师开发了一个模型，用于预测未来的市场状况。该模型看似很理想，因为它的偏差 R² 为 87%。但是，K 折叠偏差 R² 为 52%，这表明模型可能过度拟合。

高 K 折叠偏差 R² 值本身并不表示模型满足模型假设。您应该检查残差图以验证假设。

AIC、AICc 和 BIC

Akaike 信息标准 (AIC)、更正的 Akaike 信息标准 (AICc) 和 Bayesian 信息标准 (BIC) 是针对模型相对质量的度量，说明模型中的拟合与项数。

解释

使用 AIC、AICc 和 BIC 比较不同的模型。值越小越合意。但是，对于预测变量集具有最小值的模型，不一定需要很准确地拟合数据。还需要使用检验和残差图来评估模型对数据的拟合优度。

AICc 和 AIC: 当样本数量相对于模型中的参数个数较小时，AICc 的性能优于 AIC。AICc 的性能之所以更佳，是因为当模型中的参数太多时，如果样本数量相对较小，AIC 往往较小。通常，当样本数量相对于模型中的参数个数较大时，这两个统计量提供的结果相似。
AICc 和 BIC: AICc 和 BIC 评估模型的似然，然后将用来添加项的惩罚应用于模型。惩罚会降低趋势，以使模型过度拟合样本数据。趋势降低可能会生成性能通常更佳的模型。; 一般准则是，当参数个数相对于样本数量较小时，BIC 对于添加每个参数所施加的惩罚比 AICc 大。在这些情况下，最小化 BIC 的模型往往比最小化 AICc 的模型小。; 在一些常见情况（如筛选设计）下，参数个数相对于样本数量通常较大。在这些情况下，最小化 AICc 的模型往往比最小化 BIC 的模型小。例如，对于包含 13 个游程的明确筛选设计，在一组包含 6 个或多个参数的模型中，最小化 AICc 的模型往往比最小化 BIC 的模型小。; 有关 AICC 和 BIC 的更多信息，请参阅伯纳姆和安德森。¹

¹ Burnham, K. P., & Anderson, D. R. (2004)。 Multimodel inference: Understanding AIC and BIC in model selection. Sociological Methods & Research, 33(2), 261-304. doi:10.1177/0049124104268644