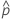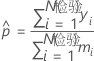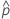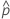请选择您所选的方法或公式。
偏差 R2
偏差 R2 表示响应变量中由模型解释的变异量。R2 越大，模型与数据拟合得越好。公式为：
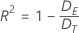
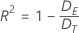
表示法
| 项 | 说明 |
|---|---|
| DE | Error Deviance |
| DT | Total Deviance |
调整的偏差 R2
调整的偏差 R2 可以说明模型中预测变量的数量，并且可用于比较具有不同预测变量数量的模型。公式为：
表示法
| 项 | 说明 |
|---|---|
| R2 | 偏差 R2 |
| p | 回归自由度 |
| Φ | 1，用于二项和 Poisson 模型 |
| DT | 总偏差 |
尽管在计算调整的偏差 R2 时可能会产生负值，但 Minitab 将针对这些情况显示零。
Akaike 信息准则 (AIC)
使用此统计量比较不同模型。AIC 越小，模型与数据拟合得越好。
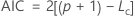
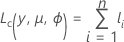
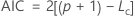
根据平均值参数化对数似然函数。函数的一般形式如下：
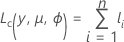
个体贡献的一般形式如下：
个体贡献的特定形式取决于模型。
| 模型 | li |
| 二项 |  |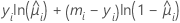
| Poisson |  |
表示法
| 项 | 说明 |
|---|---|
| p | 回归自由度 |
| Lc | 当前模型的对数似然 |
| yi | 第 i 行的事件数 |
| mi | 第 i 行的试验数 |
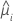 | 第 i 行的估计均值响应 |
AICc（Akaike 更正的信息标准）
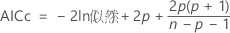
在满足以下条件时不计算 AICc：
.
表示法
| 项 | 说明 |
|---|---|
| p | 模型中系数的个数，包括常量系数 |
| n | 具有非缺失数据的行的数量 |
BIC（Bayesian 信息标准）
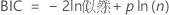
表示法
| 项 | 说明 |
|---|---|
| p | 模型中的系数，不包括常量系数 |
| n | 具有非缺失数据的行的数量 |
检验偏差 R2
检验偏差 R2 指示模型解释的检验数据集响应中的变异程度。值越高，模型与检验数据的拟合度越高。
公式
以下方程给出了检验偏差 R2 的公式：
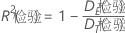
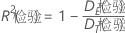
其中，以下方程表示误差偏差：
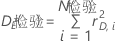
总偏差 DT（检验）的公式取决于模型的形式。
- 二值 Logistic
-
- 其中，对于具有截距项的模型，
具有以下定义： -
- 对于没有截距项的模型，请使用在 0 处的链接函数的逆。Minitab 中链接函数的值如下：
- Logit 链接函数
= 0.5。- Normit 链接函数
= 0.5。- Gompit 链接函数
。
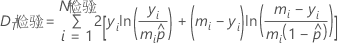
- Poisson
-
-
- 对于没有截距项的模型，
。
表示法
| 项 | 说明 |
|---|---|
| N（检验） | 检验数据集中的行数 |
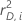 | 平方差残差 |
| yi | 检验数据集中第 i 行的事件数 |
| mi | 检验数据集中第 i 行的试验数 |
| DE（检验） | 检验数据集的误差偏差 |
| DT（检验） | 检验数据集的总偏差 |
K 折叠偏差 R2
K 折叠偏差 R2 指示模型解释的验证数据集响应中的变异程度。值越高，模型与检验数据的拟合度越高。
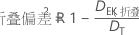
其中，
和 DT 是总偏差。
表示法
| 项 | 说明 |
|---|---|
| K | 折叠数 |
| nj | 折叠 j 的样本数量 |
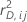 | 折叠 j 的第 i 行的交叉验证残差偏差 |
ROC 曲线下面积
公式
曲线下面积是梯形面积的总和：
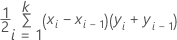
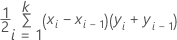
其中，k 是可区分事件概率的数量，(x0, y0) 是点 (0, 0)。
要从检验数据集或交叉验证数据中计算曲线的面积，请使用对应曲线中的点。
例如，假设在 ROC 曲线上有如下坐标的四个可区分事件概率：
| x（假阳率） | y（真阳率） |
|---|---|
| 0,0923 | 0,3051 |
| 0,4154 | 0,7288 |
| 0,7538 | 0,9322 |
| 1 | 1 |
然后，通过以下计算给出 ROC 曲线下面积：
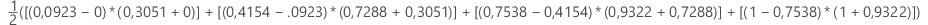
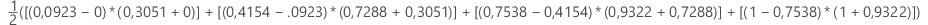
表示法
| 项 | 说明 |
|---|---|
| TRP | 真阳率 |
| FPR | 假阳率 |
| TP | 正确评估的事件的真阳性 |
| P | 实际阳性的事件数 |
| FP | 正确评估的非事件的真阴性 |
| N | 实际阴性的事件数 |
| FNR | 假阴率 |
| TNR | 真阴率 |
