系数
存在两种可以确定系数的极大似然估计的方法。一种方法是直接最大化系数对应的似然函数。这些表达式的系数呈非线性。另一种方法是使用迭代重量最小平方 (IRWLS) 方法,这是 Minitab 用于获取系数估计的方法。麦库拉和内尔德1 表明 这两种方法是等价的。但是,迭代重加权最小二乘法更易于执行。有关详细信息,请参见 1。
对于某些 K 折交叉验证情况的一步近似方法
对于具有许多交叉验证褶皱的一些大样本设计,Minitab 在交叉验证算法中使用一步近似方法来缩短计算时间(请参阅 Pregibon2 和 Williams3)。对于这些设计,折叠的培养模型与 IRWLS 算法的完全收敛不相适应,而是折叠的交叉验证统计信息来自算法第一个迭代步骤的回归参数。
下表显示了哪些设计从 1 步近似值获取交叉验证统计信息。
| 样本数量 (n) | 设计矩阵中的列数 (p) | 折叠数(k) |
|---|---|---|
| 200 < n ≤ 500 | 150 < p ≤ 300 | k > 200 |
| p = 300 | k > 100 | |
| 500 < n ≤ 1000 | 100 < p ≤ 300 | k > 300 |
| p = 300 | k > 150 | |
| 1000 < n ≤ 10,000 | p = 50 | k > 1,000 |
| 50 < p ≤ 200 | k > 200 | |
| 200 < p ≤ 400 | k > 50 | |
| p = 400 | k > 10 | |
| 10,000 < n ≤ 50,000 | p = 50 | k > 200 |
| 50 < p ≤ 200 | k > 100 | |
| p = 200 | k > 20 | |
| 50,000 < n ≤ 100,000 | p = 50 | k > 100 |
| 50 < p ≤ 150 | k > 50 | |
| p = 150 | k > 20 | |
| n = 100,000 | p 的任何值 | k > 100 |
一步近似算法
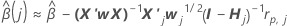
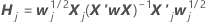
表示法
| 项 | 说明 |
|---|---|
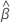 | 与完整数据集匹配的估计系数 |
| X | 完整数据集的设计矩阵 |
| X' | 完整数据集的设计矩阵的横向 |
| W | 完整数据集的重量矩阵 |
| X 'j | jth 折叠中 数据的设计矩阵 |
| Wj | jth 折叠中 数据的重量矩阵 |
| Ⅰ | 标识矩阵 |
| rp, j | j th 折叠中数据的完整数据集的模型的 Pearson 残差的矢 量 |
[1] P. 麦克库拉格和J.A.内尔德(1989年)。通用线性模型, 2和 Ed., 查普曼和霍尔 / Crc, 伦敦.
[2] D. 普雷吉邦(1981年)。逻辑回归诊断。The Annals of Statistics(统计学年刊),第 9 卷(第 4 期),第 705-724 页。
[3] D. A. 威廉姆斯(1987年)。使用偏离和单例删除的通用线性模型诊断,应用 统计,36(2),181-191。
系数的标准误
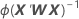
W 是对角矩阵,其中通过以下公式可以得出对角线元素的:
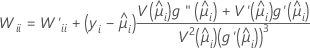
其中

此方差-协方差矩阵基于与 Fisher 的信息矩阵相对的已观测的 Hessian 矩阵。Minitab 使用已观测的 Hessian 矩阵,因为针对任何条件均值错误设定,该矩阵生成的模型更稳健。
如果使用规范链接,则已观测的 Hessian 矩阵与 Fisher 的信息矩阵相同。
表示法
| 项 | 说明 |
|---|---|
| yi | 第 i 行的响应值 |
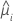 | 第 i 行的估计均值响应 |
| V(·) | 下表列出的方差函数 |
| g(·) | 链接函数 |
| V '(·) | 方差函数的一阶导数 |
| g'(·) | 链接函数的一阶导数 |
| g''(·) | 链接函数的二阶导数 |
方差函数取决于模型:
| 模型 | 方差函数 |
| 二项 | 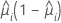 |
| Poisson | 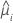 |
有关详细信息,请参见 [1] 和 [2]。
[1] A. Agresti (1990)。Categorical Data Analysis(类别数据分析)。John Wiley & Sons, Inc.
[2] P. McCullagh 和 J.A. Nelder (1992)。Generalized Linear Model(广义线性模型)。Chapman & Hall。
Z
Z 统计量用于确定预测变量是否与响应变量显著相关。Z 的绝对值越大,表示关系越显著。公式为:
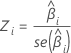
表示法
| 项 | 说明 |
|---|---|
| Zi | 标准正态分布的检验统计量 |
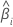 | 估计的系数 |
 | 估计系数的标准误 |
对于数量较少的样本,似然比率检验可能是更可靠的显著性检验。似然比率 P 值在偏差表中。当样本数量足够多时,Z 统计量的 P 值近似于似然比率统计量的 P 值。
P 值
用于假设检验,可帮助您确定是要否定原假设还是无法否定原假设。如果原假设成立,P 值就是获得至少与实际计算值一样极端的检验统计量的概率。P 值常用的截止值为 0.05。例如,如果检验统计量的计算的 P 值小于 0.05,您可以否定原假设。
二元 Logistic 回归的优势比
仅当您为具有二元响应的模型选择 logit 链接函数时才提供优势比。在这种情况下,优势比可用于解释预测变量与响应之间的关系。
优势比 (τ) 可以是任何非负数。优势比 = 1 时可用作比较的基线。如果 τ = 1,则响应和预测变量之间不存在关联。如果 τ < 1,则因子的参考水平(或连续预测变量的更低水平)的事件优势较高。如果 τ > 1,则因子的参考水平(或连续预测变量的更低水平)的事件优势较小。值距离 1 越远表示关联度越大。
注意
对于具有一个协变量或因子的二元 Logistic 回归模型,估计的成功几率为:
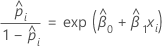
指数关系可为 β 提供解释:x 每增加一个单位,优势就成倍增加 eβ1。优势比等于 exp(β1)。
例如,如果 β 为 0.75,则优势比为 exp(0.75),即 2.11。这意味着 x 每增加一个单位,成功优势就增加 111%。
表示法
| 项 | 说明 |
|---|---|
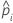 | 数据中第 i 行的估计成功概率 |
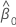 | 估计的截距系数 |
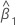 | 预测变量 x 的估计系数 |
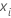 | 第 i 行的数据点 |
置信区间
估计系数的大样本置信区间为:
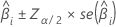
对于二项 Logistic 回归,Minitab 提供优势比的置信区间。要获得优势比的置信区间,请对置信区间的上下限取指数。该区间为预测变量的每个单位变化提供优势比可能会落入的范围。
表示法
| 项 | 说明 |
|---|---|
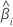 | 第 i 个系数 |
 | 标准正态分布在 处的逆累积概率 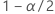 |
 | 显著性水平 |
 | 估计系数的标准误 |
方差-协方差矩阵
d x d 矩阵,其中,d 为预测变量数加一。每个系数的方差在对角线单元中,每对系数的协方差在相应的非对角线单元中。方差是系数标准误的平方。
方差-协方差矩阵来自信息矩阵的逆矩阵的最后一次迭代。方差-协方差矩阵具有以下形式:
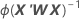
W 是对角矩阵,其中通过以下公式可以得出对角线元素:

其中

此方差-协方差矩阵基于与 Fisher 的信息矩阵相对的已观测的 Hessian 矩阵。Minitab 使用已观测的 Hessian 矩阵,因为针对任何条件均值错误设定,该矩阵生成的模型更稳健。
如果使用规范链接,则已观测的 Hessian 矩阵与 Fisher 的信息矩阵相同。
表示法
| 项 | 说明 |
|---|---|
| yi | 第 i 行的响应值 |
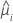 | 第 i 行的估计均值响应 |
| V(·) | 下表列出的方差函数 |
| g(·) | 链接函数 |
| V '(·) | 方差函数的一阶导数 |
| g'(·) | 链接函数的一阶导数 |
| g''(·) | 链接函数的二阶导数 |
方差函数取决于模型:
| 模型 | 方差函数 |
| 二项 | 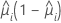 |
| Poisson | 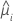 |
有关详细信息,请参见 [1] 和 [2]。
[1] A. Agresti (1990)。Categorical Data Analysis(类别数据分析)。John Wiley & Sons, Inc.
[2] P. McCullagh 和 J.A. Nelder (1992)。Generalized Linear Model(广义线性模型)。Chapman & Hall。
