请选择您所选的方法或公式。
方差分析
偏差可以度量当前模型和全模型之间的不一致。全模型是具有 n 个参数的模型,每个观测值对应一个参数。全模型可以最大化对数似然函数。全模型为少于 n 个参数的模型提供比较点。全模型比较使用尺度化的偏差。


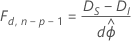

对每个单独数据点的尺度化偏差的贡献取决于模型。
| 模型 | 偏差 |
|---|---|
| 二项 | 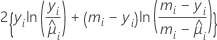 |
| 双 Poisson | 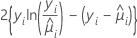 |
根据以下一般结果(假设 ϕ 已知)构造偏差表。如果 DI 是与初始模型相关的偏差,DS 是与初始模型中项的子组相关的偏差,则在某些正则性条件下,存在以下关系:

偏差之间的差分按具有 d 个自由度的卡方分布渐近分布。可以为调整的(III 型)分析和序贯(I 型)分析计算这些统计量。调整的偏差和偏差表中的卡方统计量相等。调整的均值偏差为调整的偏差除以自由度。
对于序贯分析,输出取决于预测变量输入模型的顺序。序贯偏差是预测变量解释的唯一一个偏差(假设模型中存在任意预测变量)。如果模型有 X1、X2 和 X3 三个预测变量,则 X3 的序贯偏差表示 X3 解释的剩余偏差量(假设模型中已存在 X1 和 X2)。要获得其他序贯偏差,请重复执行回归过程(按其他顺序输入预测变量)。
如果 ϕ 已知,对于遵循正态分布的响应变量,在某些正则性条件下,关系将发生变化,如下所示:
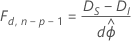
其中,偏差之间的差分按具有 d 个分子自由度和 n − p 个分母自由度的 F 分布渐近分布。要估计离差参数,请使用初始模型。
表示法
| 项 | 说明 |
|---|---|
| yi | 第 i 行的事件数 |
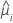 | 第 i 行的估计均值响应 |
| mi | 第 i 行的试验数 |
| Lf | 全模型的对数似然 |
| Lc | 具有全模型中项的子组的模型的对数似然 |
| d | 自由度是要比较的模型中的多个参数之间的差分 |
| ϕ | 离差参数,已知为 1,用于二项和 Poisson 模型 |
| n | 数据中的行数 |
| p | 初始模型的回归自由度 |
自由度
表示独立信息的条数,这些信息包括计算调整的均值偏差所需的响应数据。模型的每个分量的自由度为:
| 变异源 | 自由度 |
| 回归 | p |
| 误差 | n − p − 1 |
| 合计 | n − 1 |
| 连续预测变量 | 1 |
| 类别预测变量 | q − 1 |
表示法
| 项 | 说明 |
|---|---|
| p | 预测变量的自由度的总和。这些预测变量不包括常量。 |
| n | 数据集中观测值的数量。 |
| q | 类别预测变量的水平数 |
对数似然
根据平均值参数化对数似然函数。函数的一般形式如下:
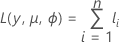

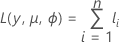
个体贡献的一般形式如下:

个体贡献的特定形式取决于模型。
| 模型 | li |
| 二项 | 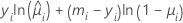 |
| Poisson | 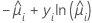 |
表示法
| 项 | 说明 |
|---|---|
| yi | 第 i 行的事件数 |
| mi | 第 i 行的试验数 |
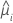 | 第 i 行的估计均值响应 |
P 值
用于假设检验,可帮助您确定是要否定原假设还是无法否定原假设。如果原假设成立,P 值就是获得至少与实际计算值一样极端的检验统计量的概率。P 值常用的截止值为 0.05。例如,如果检验统计量的计算的 P 值小于 0.05,您可以否定原假设。
