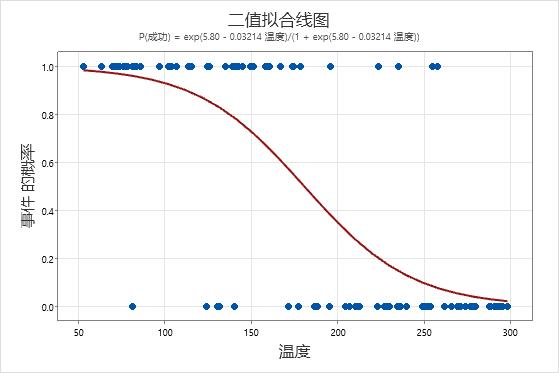
二元拟合线图
拟合线图显示响应变量和预测变量数据。该图包含回归线,代表回归方程。您也可以选择显示拟合值的置信区间。
解释
使用拟合线图可以检查响应变量与预测变量之间的关系。
在这些结果中,将方程写入为成功概率。y 轴上的响应值 1 代表成功。该图显示成功概率随温度升高而递减。当数据中的温度接近 50 时,线斜率不是很大,这表明概率随温度升高而缓慢递减。如果温度数据中间部分的线倾斜度较大,则表明 1 度的温度变化会对此范围产生较大影响。当成功概率在高温范围接近于零时,则线会再次趋于平直。
如果模型与数据非常拟合,则高预测概率显示何处的事件较为普遍。当数据中的温度接近 50 时,响应值 1 最为普遍。随着温度升高,响应值 0 变得较为普遍。
如果向该图中添加置信区间,则可以使用置信区间评估拟合估计值的精确程度。在下面的第一张图中,当预测变量增大时,置信区间线的宽度大致不变。在第二张图中,当预测变量值增大时,置信区间变宽。当温度较高时,区间变宽的部分原因是数据较少。


残差的直方图
残差偏差的直方图显示所有观测值的残差分布。
解释
| 模式 | 模式的含义 |
|---|---|
| 朝着一个方向的长尾 | 偏度 |
| 远离其他条形的条形 | 异常值 |
因为直方图的外观取决于用来进行数据分组的区间数,所以请勿使用直方图评估残差的正态性。取而代之,可使用正态概率图。
残差的正态概率图
残差的正态概率图显示,当分布呈正态时,残差与期望值的关系。
解释
使用残差正态概率图可验证残差呈正态分布的假设。残差的正态概率图应该大致为一条直线。
S 曲线表示长尾分布。
反向 S 曲线表示短尾分布。
向下的曲线表示右偏斜分布。
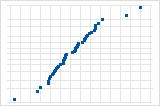
远离线的几个点表示分布中有异常值。
如果发现非正态模式,请使用其他残差图检查该模型是否存在其他问题,例如,缺失项或时间顺序效应。如果残差不遵循正态分布,则正态近似置信区间和 Wald 检验 P 值可能不准确。
残差与拟合值
残差与拟合值图形分别在 y 轴和 x 轴上绘制残差和拟合值。当数据为事件/试验格式时,此图非常有用。当数据为二进制响应/频率格式时,Minitab 不提供此图。
解释
使用残差与拟合值图可验证残差随机分布的假设。理想情况下,点应当在 0 的两端随机分布,点中无可辨识的模式。
| 模式 | 模式的含义 |
|---|---|
| 残差相对拟合值呈扇形或不均匀分散 | 不合适的链接函数 |
| 曲线 | 缺少高阶项或不合适的链接函数 |
| 远离 0 的点 | 异常值 |
| 在 X 方向远离其他点的点 | 有影响的点 |

含异常值的图
其中一个点比所有其他点大得多。因此,该点是异常值。如果异常值过多,则模型可能不可接受。您应该尝试找出导致任何异常值的原因。更正任何数据输入错误或测量误差。考虑删除与异常的单次事件(也称为特殊原因)相关联的数据值。然后,重新执行分析。
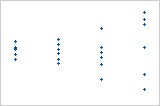
含异方差的图
残差的方差随拟合值增加。请注意,随着拟合值增大,残差之间的散布变宽。此模式表示残差的方差不相等(非恒定)。
| 问题 | 可能解决方案 |
|---|---|
| 异方差 | 考虑使用模型中的不同项、不同的链接函数或权重。 |
| 异常值或有影响的点 |
|
残差与顺序
残差与顺序图按照数据的收集顺序显示残差。
解释
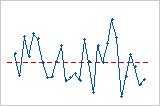
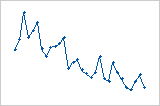
趋势
偏移
周期
残差与变量
残差与变量的关系图显示残差与另一个变量的关系。已在模型中包含此变量。或者,模型中未包含此变量,但是猜测它会影响响应。
解释
如果在残差中看到非随机图形,则表明变量会系统性地影响响应。请考虑在分析中包含此变量。
