一位医学研究人员想了解一种新药的剂量水平对成人体内细菌的影响。该研究人员进行了一项试验,该试验有 30 位患者参与并包含 6 种剂量水平。在两周内,研究人员给 5 名患者服用了一种剂量水平,给另外 5 名患者服用了另一种剂量水平,以此类推。在两周的周期结束时,对每名患者进行了检验,以确定是否能检测到任何细菌。
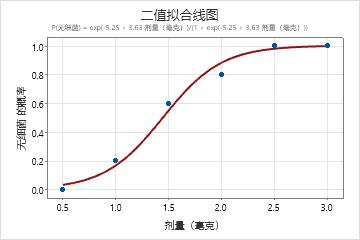
由于该数据包含一个二元响应和一个连续预测变量,因此该研究人员使用二元拟合线图确定药物的剂量与细菌的有无是否相关。
- 打开样本数据 抗菌药.MWX。
- 选择。
- 从下拉列表中,选择事件/试验格式的响应。
- 在事件名称中,键入无细菌。
- 在事件数中,输入“无细菌”。
- 在试验数中,输入试验。
- 在预测变量中,输入“剂量(毫克)”。
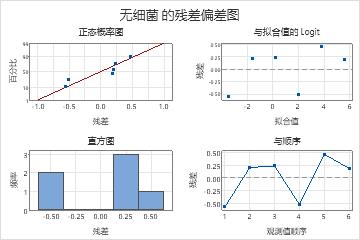
- 单击图形。在残差图下,选择四合一。
- 单击每个对话框中的确定。
解释结果
药物剂量的 P 值小于显著性水平 0.05。这些结果表示药物剂量和是否存在细菌之间的关系在统计上显著。二元拟合线图显示当剂量增大时,不存在细菌的可能性将变大。此外,优势比表示剂量水平每增加 1 毫克,不存在细菌的可能性将增加约 38 倍。拟合线图显示模型可以较好地拟合数据,而残差图显示模型不存在任何问题。
方法
| 链接函数 | Logit |
|---|---|
| 已使用的行数 | 6 |
响应信息
| 变量 | 值 | 计数 | 事件名称 |
|---|---|---|---|
| 无细菌 | 事件 | 18 | 无细菌 |
| 非事件 | 12 | ||
| 试验 | 合计 | 30 |
回归方程
| P(无细菌) = exp(-5.25 + 3.63 剂量(毫克))/(1 + exp(-5.25 + 3.63 剂量(毫克))) |
|---|
系数
| 项 | 系数 | 系数标准误 | 方差膨胀因子 |
|---|---|---|---|
| 常量 | -5.25 | 1.99 | |
| 剂量(毫克) | 3.63 | 1.30 | 1.00 |
连续预测变量的优势比
| 优势比 | 95% 置信区间 | |
|---|---|---|
| 剂量(毫克) | 37.5511 | (2.9647, 475.6190) |
模型汇总
| 偏差 R-Sq | 偏差 R-Sq (调整) | AIC | AICc | BIC |
|---|---|---|---|---|
| 96.04% | 91.81% | 10.63 | 14.63 | 10.22 |
方差分析
| 来源 | 自由度 | 调整后偏差 | 调整后均值 | 卡方 | P 值 |
|---|---|---|---|---|---|
| 回归 | 1 | 22.7052 | 22.7052 | 22.71 | 0.000 |
| 剂量(毫克) | 1 | 22.7052 | 22.7052 | 22.71 | 0.000 |
| 误差 | 4 | 0.9373 | 0.2343 | ||
| 合计 | 5 | 23.6425 |