注意
此命令适用于 预测分析模块。单击此处了解更多关于如何激活模块的信息。
TreeNet® 模型是解决分类和回归问题的方法,与单一分类或回归树相比,既准确又不易过度拟合。宽泛而言,在该过程刚开始时我们将使用一个小回归树作为初始模型。从该树上,数据中的每一行都有残差,这些残差成为下一个回归树的响应变量。我们构建另一个回归小树来预测第一个树的残差并再次计算产生的残差。我们重复此序列,直到使用验证方法确定具有最小预测误差的最优树数量。生成的树序列形成 TreeNet® 回归模型。
对于回归案例,我们可以添加分析的一般说明,但一些详细信息取决于以下哪种是损失函数:
| 统计量 | 文字转数字 (Value) |
|---|---|
初始拟合,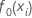
|
响应变量的均值 |
广义残差,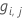 作为第
i 行的响应值
作为第
i 行的响应值
|

|
在节点更新中,
|
的均值 
|
| 统计量 | 文字转数字 (Value) |
|---|---|
初始拟合,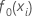
|
响应变量的中位数 |
广义残差,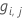 作为第
i 行的响应值
作为第
i 行的响应值
|
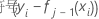
|
在节点更新中,
|
的中位数
|
Huber 损失函数
对于 Huber 损失函数,统计量如下:
初始拟合,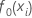 ,等于所有响应值的中位数。
,等于所有响应值的中位数。
为了生成第 j 个树,
之后,第 i 行的广义残差如下所示:
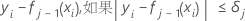

广泛残差用作响应值,以生成第 j 个树。
第 j 个树的第 m 个终端节点中行的更新值如下:
定义  是
j-1 个树生成之后第
i 行的正规残差。设
是
j-1 个树生成之后第
i 行的正规残差。设 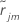 是
是 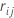 第
j 个树的终端节点
m 中各行的 值的中位数那么,第
j 个树的第
m 个终端节点中每行的更新值是:
第
j 个树的终端节点
m 中各行的 值的中位数那么,第
j 个树的第
m 个终端节点中每行的更新值是: 
 是
j-1 个树生成之后第
i 行的正规残差。设
是
j-1 个树生成之后第
i 行的正规残差。设 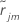 是
是 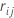 第
j 个树的终端节点
m 中各行的 值的中位数那么,第
j 个树的第
m 个终端节点中每行的更新值是:
第
j 个树的终端节点
m 中各行的 值的中位数那么,第
j 个树的第
m 个终端节点中每行的更新值是: 
在第 j 个树的终端节点 m 内的所有行中计算前面表达式中的平均值。
损失函数的表示法
在前面的详细信息中,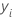 是第
i 行的响应变量的值,
是第
i 行的响应变量的值, 是前面的
j – 1 树的拟合值,而
是前面的
j – 1 树的拟合值,而 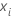 是代表训练数据中预测变量值的第
i 行的矢量。
是代表训练数据中预测变量值的第
i 行的矢量。
输入参数
创建模型时还会使用来自分析人员的以下输入:
| 输入 | 符号 |
|---|---|
| 学习速率 |  |
| 抽样率 | 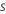 |
| 每个树的最大终端节点数 | 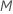 |
| 树数 | 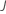 |
| 切换值 |  |
一般过程
该过程有以下一般步骤来生成第
j 个树,j = 1, ...,
J:
- 从训练数据中抽取数量为 s * N 的随机样本,其中 N 是训练数据中的行数。
- 计算广义残差
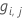 (对于
(对于
 )。
)。
- 将最多具有 M 个终端节点的回归树与广义残差拟合。该树将观测值最多分割为 M 个互斥组。
- 对于回归树中的第
m 个终端节点,计算依赖于损失函数的树的节点内更新数(
 )。
)。
- 按学习速率减少节点内更新数,并应用这些值以获取经过更新的拟合值,
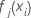 ):
):
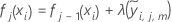
- 对分析中的每个 J 树,重复步骤 1 到 5。
