Minitab® 支持

TreeNet® 回归的 拟合模型 示例

了解关于 Minitab 的更多信息
注意

此命令适用于 预测分析模块。单击此处了解更多关于如何激活模块的信息。

一个研究小组希望使用有关借款人和房产位置的数据来预测抵押金额。变量包括借款人的收入、种族和性别，以及房产的人口普查区位置和其他有关借款人和房产类型的信息。

经过初步探索用于确定重要预测变量的 CART® 回归，团队现在考虑将 TreeNet® 回归 作为必要的后续步骤。研究人员希望更深入地了解响应与重要预测变量之间的关系，并且更准确地预测新观测值。

这些数据根据一个包含有关联邦住房贷款银行抵押信息的公共数据集进行了改编。原始数据来自 fhfa.gov。

  1. 打开样本数据集购买抵押.MTW。
  2. 选择 预测分析模块 > TreeNet® 回归 > 拟合模型。
  3. 在 响应中，输入贷款金额。
  4. 在 连续预测变量 中，输入 年收入 – 地区收入。
  5. 在 类别预测变量 中，输入 首次购房者 – 基于核心的统计区域。
  6. 单击 验证。
  7. 在验证方法中，选择 K 折叠交叉验证。
  8. 在折叠数 (K)中，输入 3。
  9. 单击每个对话框中的确定。

解释结果

对于此分析，Minitab 生成 300 个树，最优树数为 300。由于最优树数接近模型生成的最大树数，研究人员使用更多树重复运行分析。

TreeNet® 回归： 贷款金额 vs 年收入, 收入比率, 前端比率, 后端比率, 借款人数量, 年龄, 共同借款人年龄, 普查区少数族裔百分比, ...

模型汇总 总预测变量 34 重要预测变量 19 增长的树数 300 最优树数 300 统计量 训练 测试 R 平方 94.02% 84.97% 均方根误差 (RMSE) 32334.5587 51227.9431 均方误差 (MSE) 1045523683.1610 2624302154.9887 平均绝对偏差 (MAD) 22740.1020 35974.9695 平均绝对百分比误差 (MAPE) 0.1238 0.1969

使用 500 个树的示例

  1. 在模型汇总表后，单击 调整超参数以确定更好的模型。
  2. 在 树数 中，输入 500。
  3. 单击 显示结果。

解释结果

对于这个分析，生成了 500 个树，具有准确度标准最佳值的超参数组合的最优树数是 500。子样本部分更改为 0.7，而不是原始分析中的 0.5。在原始分析中，学习速率更改为 0.0437，而不是 0.04372。

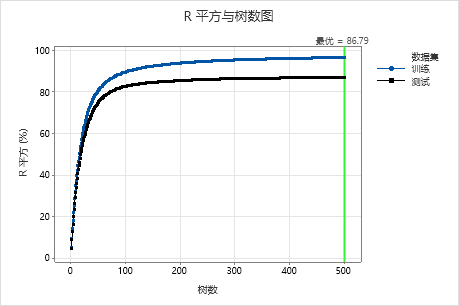
检查模型汇总表和 R 平方与树数图。当树数为 500 时，R2 值对于测试数据为 86.79%，对于训练数据为 96.41%。这些结果与传统的回归分析和 CART® 回归 相比有所改进。

TreeNet® 回归： 贷款金额 vs 年收入, 收入比率, 前端比率, 后端比率, 借款人数量, 年龄, 共同借款人年龄, 普查区少数族裔百分比, ...

方法 损失函数 平方误差 选择最优树数量的标准 最大 R 平方 模型验证 3 折叠交叉验证 学习速率 0.04372 子样本部分 0.5 每个树的最大终端节点数 6 最小终端节点大小 3 为进行节点拆分而选定的预测变量数 预测变量总数 = 34 已使用的行数 4372
响应信息 均值 标准差 最小值 下四分位数 中位数 上四分位数 最大值 235217 132193 23800 136000 208293 300716 1190000

具有超参数调整的 TreeNet® 回归: 贷款金额 与 年收入, 收入比率, 前端比率, 后端比率, 借款人数量, 年龄, 共同借款人年龄, ...

方法 损失函数 平方误差 选择最优树数量的标准 最大 R 平方 模型验证 3 折叠交叉验证 学习速率 0.001, 0.0437, 0.1 子样本部分 0.5, 0.7 每个树的最大终端节点数 6 最小终端节点大小 3 为进行节点拆分而选定的预测变量数 预测变量总数 = 34 已使用的行数 4372
响应信息 均值 标准差 最小值 下四分位数 中位数 上四分位数 最大值 235217 132193 23800 136000 208293 300716 1190000
超参数优化 测试 模型 最优树数 R 平方 (%) 平均绝对偏差 学习速率 子样本部分 最大终端节点数 1 500 36.43 82617.1 0.0010 0.5 6 2 495 85.87 34560.5 0.0437 0.5 6 3 495 85.63 34889.3 0.1000 0.5 6 4 500 36.86 82145.0 0.0010 0.7 6 5* 500 86.79 33052.6 0.0437 0.7 6 6 451 86.67 33262.3 0.1000 0.7 6 * 最优模型具有最大 R 平方。最优模型的输出如下。

TreeNet® 回归： 贷款金额 vs 年收入, 收入比率, 前端比率, 后端比率, 借款人数量, 年龄, 共同借款人年龄, 普查区少数族裔百分比, ...

模型汇总 总预测变量 34 重要预测变量 24 增长的树数 500 最优树数 500 统计量 训练 测试 R 平方 96.41% 86.79% 均方根误差 (RMSE) 25035.7243 48029.9503 均方误差 (MSE) 626787491.1374 2306876123.1055 平均绝对偏差 (MAD) 17309.3936 33052.6087 平均绝对百分比误差 (MAPE) 0.0930 0.1790

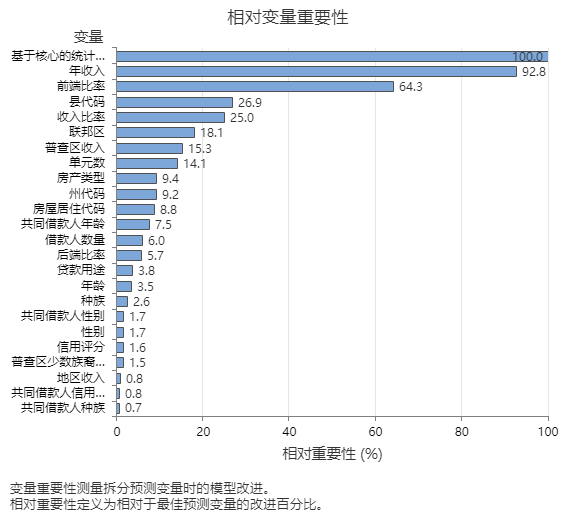
相对变量重要性图按照在对树序列上的预测变量进行拆分时预测变量对模型的改进作用的顺序，绘制预测变量的重要性图。最重要的预测变量是基于核心的统计区域。如果顶部预测变量（基于核心的统计区域）的重要性为 100%，则下一个重要变量“年收入”的贡献率为 92.8%。这意味着借款人的年收入与房产的地理位置一样重要。

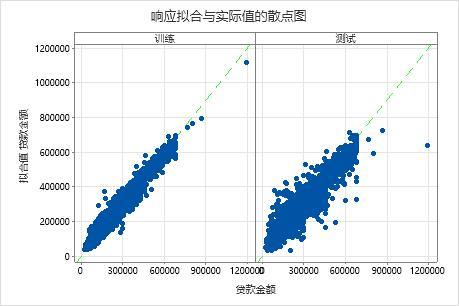
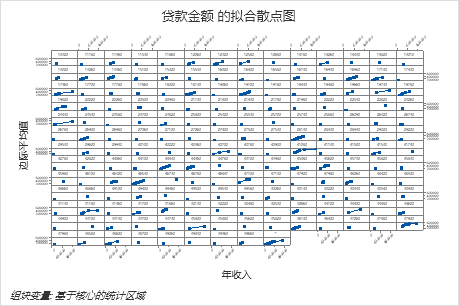
拟合贷款金额与实际贷款金额的散点图显示训练数据和检验数据的拟合值和实际值之间的关系。您可以将鼠标悬停在图形上的点上，以便更轻松地查看标绘的值。在此示例中，所有点都大约分布在参考线 y=x 附近。

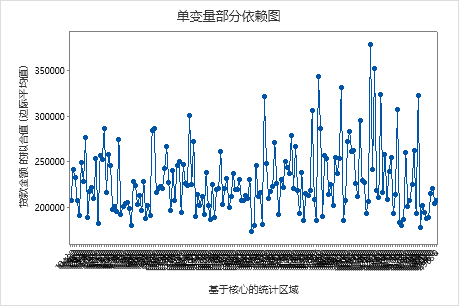
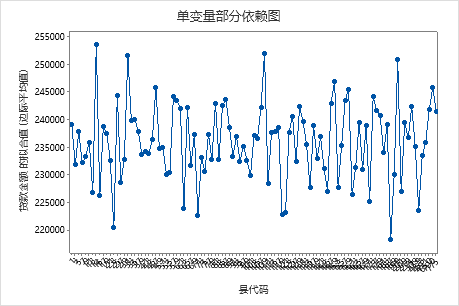
使用部分依赖图可以深入了解重要变量或变量对如何影响拟合响应值。部分依赖图显示响应与变量之间的关系是线性、单调还是更复杂的关系。

第一个图说明了每个基于核心的统计区域的拟合贷款金额。由于数据点太多，因此您可以将鼠标悬停在各个数据点上以查看特定的 x 值和 y 值。例如，图形右侧的最高点对应于核心区域号 41860，拟合贷款金额约为 378069 美元。

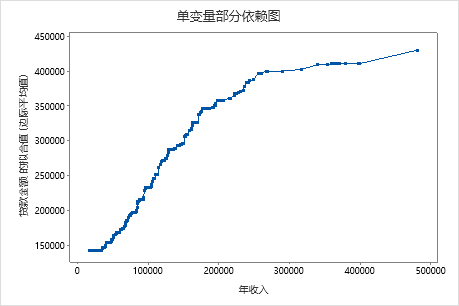
第二个图说明，拟合贷款金额随着年收入的增加而增加。年收入达到30万元后，贷款金额水平增长较慢。

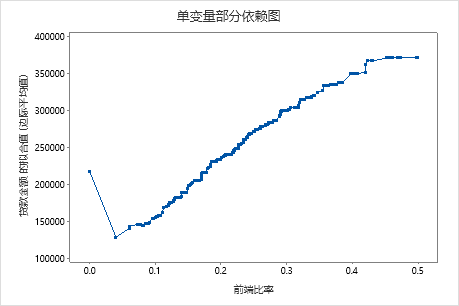
第三个图说明，拟合贷款金额随着前端比率的增加而增加。

第四个图说明了每个人口普查县代码的拟合贷款金额。与第一个图一样，您可以将鼠标悬停在某些数据点上以获取更多信息。单击 选择更多要绘制的预测变量 以生成其他变量的图。

Copyright © 2024 Minitab, LLC. All rights Reserved.