注意
此命令适用于 预测分析模块。单击此处了解更多关于如何激活模块的信息。
一组研究人员从位于爱荷华州艾姆斯的个人住宅物业的出售中收集数据。研究人员希望找出影响销售价格的变量。变量包括住宅物业的地块大小和各种功能。
使用 CART® 回归 进行初步探索以确定重要预测变量后,团队使用 Random Forests® 回归 从同一数据集创建更密集的模型。团队根据结果比较模型汇总表和 R2 图,以评估哪个模型可提供更好的预测结果。
这些数据根据一个包含有关艾姆斯住房数据的公共数据集进行了改编。来自杜鲁门州立大学 DeCock 的原始数据。
- 打开样本数据 艾姆斯住房.MWX。
- 选择 。
- 在响应中,输入’销售价格’。
- 在 中 连续预测变量,输入’地段正面’ – ‘销售年份’。
- 在 中 类别预测变量,输入’类型’ – ‘销售条件’。
- 单击 选项。
- 在 节点分裂的预测变量数 下,选择 预测变量总数的百分 K;K =,然后输入 30。 研究人员希望使用超过默认数量的预测变量数进行此分析。
- 单击每个对话框中的确定。
解释结果
对于此分析,观测值个数为 2930。300 个 Bootstrap 样本中的每个样本随机选择 2930 个观测值,进行替换,以创建树。该方法还使用预测变量总数的 30%
来拆分节点。此外,响应信息表显示观测值的常见描述性统计量。
方法
| 模型验证 | 使用 OOB 数据进行验证 |
|---|---|
| Bootstrap 样本数 | 300 |
| 样本数量 | 与 2930 的训练数据大小相同 |
| 为进行节点拆分而选定的预测变量数 | 预测变量总数的 30% = 23 |
| 最小内部节点大小 | 5 |
| 已使用的行数 | 2930 |
响应信息
| 均值 | 标准差 | 最小值 | 下四分位数 | 中位数 | 上四分位数 | 最大值 |
|---|---|---|---|---|---|---|
| 180796 | 79886.7 | 12789 | 129500 | 160000 | 213500 | 755000 |
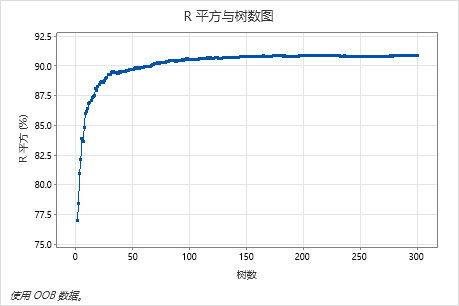
R 平方与树数图显示生成的树数的整个曲线。R2 值随着树数量的增加而迅速增加,然后在大约 91% 处趋于平坦。
模型汇总
| 总预测变量 | 77 |
|---|---|
| 重要预测变量 | 68 |
| 统计量 | OOB |
|---|---|
| R 平方 | 90.90% |
| 均方根误差 (RMSE) | 24097.3281 |
| 均方误差 (MSE) | 5.80681E+08 |
| 平均绝对偏差 (MAD) | 14746.8323 |
| 平均绝对百分比误差 (MAPE) | 0.0895 |
模型汇总表显示 R2 值与相应的 CART® 分析的 R2 值相比略有改进。
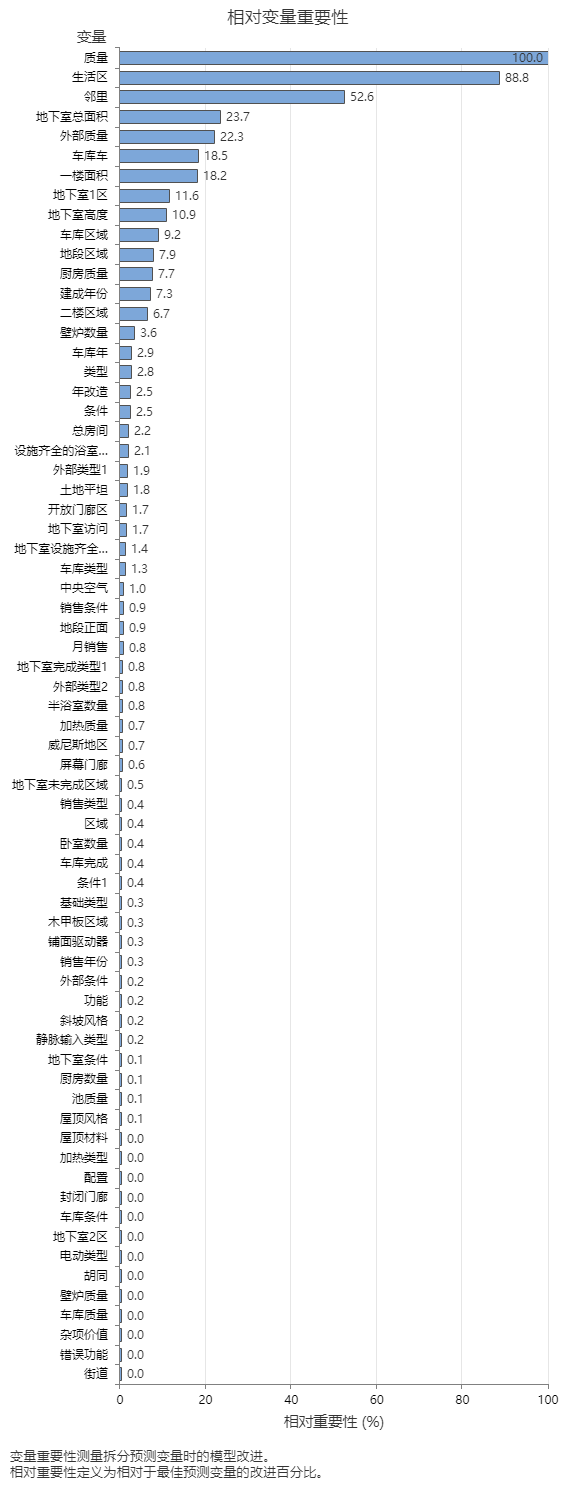
相对变量重要性图按照在对树序列上的预测变量进行拆分时预测变量对模型的改进作用的顺序,绘制预测变量的重要性图。预测销售价格的最重要预测变量是“质量”。如果顶部预测变量质量的重要性为 100%,则下一个重要变量 生活区 的贡献为 88.8%。这意味着居住的平方英尺与房产的整体质量一样重要88.8%。下一个最重要的变量是邻域,其贡献率为52.6%。
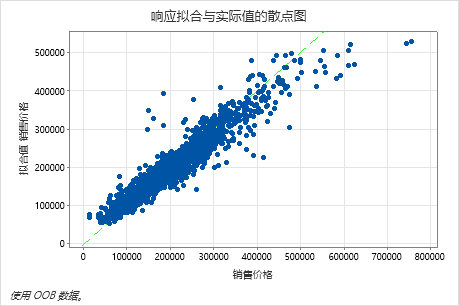
拟合销售价格与实际销售价格的散点图显示了 OOB 数据的拟合值与实际值之间的关系。您可以将鼠标悬停在图形上的点上,以便更轻松地查看标绘的值。在此示例中,许多点大约落在 y=x 的参考线附近,但有几个点可能需要调查才能看到拟合值和实际值之间的差异。
