注意
此命令可用于预测分析模块。单击此处了解更多关于如何激活模块的信息。
MARS® 回归 本质上是通过拟合分段线性回归来构建灵活的模型。该模型的限制是分段线的端点均匀连接。模型非线性的近似值在不同的数据区间内使用单独的回归斜率。在简单的二维情况下,该过程的近似值很容易可视化。
在二维情况下,一条直线拟合数据。此模型为测试增加额外复杂性的改进提供了基线。
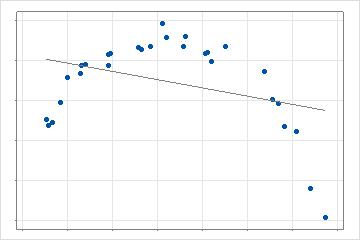
在下一步中,分析将搜索预测变量的值,该预测变量创建基础函数,从而最大程度地改进搜索条件。准则的计算取决于分析的选择和验证方法。在二维情况下,此模型是分段线性回归,具有 2 条线而不是 1 条线。对于多个预测变量,搜索最佳数据点将评估分析允许的每个预测变量。
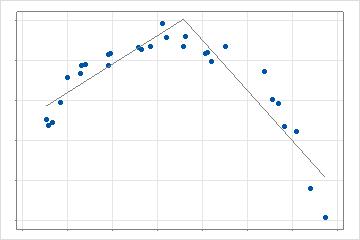
分析找到提供最佳改进的第一个值后,分析将搜索剩余的预测变量值以查找当前模型的最佳改进。在二维情况下,此模型有 3 行描述数据的不同部分。搜索将重复到分析的最大基函数数。当允许交互作用时,分析通过将候选基函数与模型中已存在的其他基函数相乘来执行额外的一系列搜索。
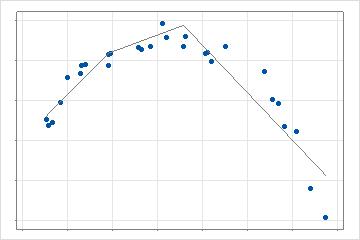
在分析快速拟合最大基函数数并估计这些函数的参数后,分析将确定基函数的最佳数量。最优基函数数使用逐步、向后消除方法来查找具有最优性准则最佳值的基函数数。
模型拟合的缺失值
在搜索基函数时, MARS® 回归 为任何具有缺失值的预测变量创建指示变量。指示符变量显示是否缺少预测变量的值。如果分析包括模型中具有缺失值的预测变量的基础函数,则模型还包括指示变量的基础函数。预测变量的其他基函数都与指示变量的基函数交互。
当预测变量具有缺失值时,指示变量的基础函数通过乘以 0 使该预测变量的其他基础函数无效。缺失值的这些基函数存在于重要预测变量具有缺失值的所有模型中,甚至是加法模型和禁用其他类型的变换的模型。
预测的缺失值
MARS® 回归 当模型中的预测变量具有缺失值时计算预测。分析使用不同的策略,具体取决于分析拟合模型时预测变量的缺失值是否存在。如果分析拟合模型时存在预测变量的缺失值,则模型中的基础函数包括一个指示变量,当预测变量具有缺失值时,该指示变量将从模型中删除预测变量。
第二种情况是预测值包括预测变量的缺失值,但在分析拟合模型时预测变量没有缺失值。在这种情况下,为了计算预测值,分析将插补缺失值。对于连续预测变量,预测变量的均值将替换缺失值。对于类别预测变量,数据集中的最终非缺失值将替换缺失值。
