步骤 1:确定模型与数据的拟合优度
- 检验 R 平方
- R2 值越高,模型与数据的拟合度越好。R2 始终介于 0% 和 100% 之间。异常值对 R2 的影响比对 MAD 的影响大。
- 检验均方根误差 (RMSE)
- 值越小,拟合越好。异常值对 RMSE 的影响比对 MAD 的影响大。
- 检验均方误差 (MSE)
- 值越小,拟合越好。异常值对 MSE 的影响比对 MAD 的影响大。
- 检验平均绝对偏差 (MAD)
- 值越小,拟合越好。平均绝对偏差 (MAD) 以与数据相同的单位表示准确度,这有助于使误差量概念化。异常值对 MAD 的影响小于对 R2、RMSE 和 MSE 的影响。
模型汇总
| 总预测变量 | 77 |
|---|---|
| 重要预测变量 | 10 |
| 基函数的最大数量 | 30 |
| 基函数的最优数量 | 13 |
| 统计量 | 训练 | 测试 |
|---|---|---|
| R 平方 | 89.61% | 87.61% |
| 均方根误差 (RMSE) | 25836.5197 | 27855.6550 |
| 均方误差 (MSE) | 667525749.7185 | 775937512.8264 |
| 平均绝对偏差 (MAD) | 17506.0038 | 17783.5549 |
关键结果:检验 R 平方、检验均方根误差 (RMSE)、检验均方误差 (MSE)、检验均值绝对偏差 (MAD)
在这些结果中,检验 R 平方约为 88%。检验均方根误差约为 27,856。检验均方误差约为 775,937,513。检验平均绝对偏差约为 17,784。
步骤 2:确定哪些变量对模型最重要
使用相对变量重要性图表可以查看哪些预测变量是模型最重要的变量。
重要变量在模型中至少位于 1 个基函数中。改进得分最高的变量设置为最重要的变量,其他变量依次排序。相对变量重要性将重要性值标准化,以便于解释。相对重要性定义为相对于最重要预测变量的改进百分比。
相对变量重要性值的范围为 0% 到 100%。最重要的变量始终具有 100% 的相对重要性。如果变量不在基函数中,则该变量不重要。
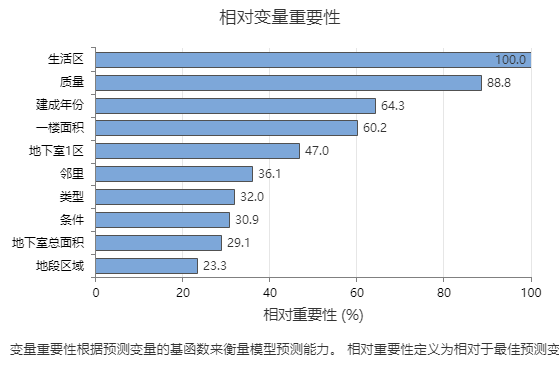
关键结果:相对变量重要性
- 质量 的重要性约为 生活区的 89%。
- 建成年份 的重要性约为 生活区的 64%。
- 一楼面积 的重要性约为 生活区的 60%。
尽管这些结果包含 10 个重要性为正的变量,但可以根据相对排名来确定针对特定应用要控制或监控多少个变量。如果相对重要性值从一个变量到下一个变量存在大幅下降,则可以据此决定要控制或监控哪些变量。例如,在这些数据中,两个最重要的变量的重要性值在相对于下一个变量的相对重要性下降 20% 以上之前相对接近。同样,2 个变量的重要性值相似,超过 60%。您可以从不同的组中删除变量并重做分析,以评估各个组中的变量如何影响模型汇总表中的预测准确度值。
步骤 3:探索预测变量的效应
使用回归方程中的部分依赖图、基函数和系数来确定预测变量的效应。预测变量的效应解释了预测变量和响应变量之间的关系。考虑预测变量的所有基函数,以了解预测变量对响应变量的影响。
此外,在构建其他模型时,请考虑重要预测变量的使用及其关系形式。例如,如果 MARS® 回归模型包括交互作用,请考虑是否将这些交互作用包含在最小二乘回归模型中,以比较两种类型的模型的性能。在控制预测变量的应用程序中,效应提供了一种自然的方式来优化设置以实现响应变量的目标。
在加性模型中,单预测变量部分依赖图显示重要的连续预测变量如何影响预测响应。一个预测变量偏相关性图指示预期响应如何随预测变量水平的变化而变化。对于 MARS® 回归,图上的值来自 x 轴上预测变量的基础函数。y 轴上的贡献是标准化的,因此图上的最小值为 0。
关键结果:部分依赖图
该图说明了随着 销售价格 数据集中最小平方英尺增加到约 3,000 平方英尺而 生活区 增加。在达到3,000平方英尺后 生活区 ,捐款 销售价格 将保持不变,约为152,000美元。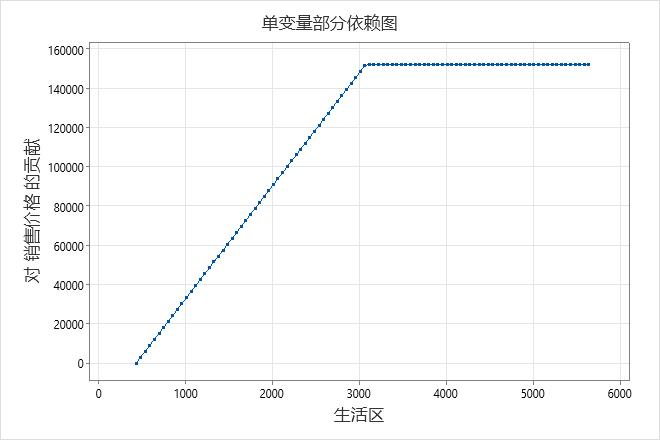
回归方程
BF3 = 当 质量 为 8, 9, 10 时
BF6 = max(0, 2002 - 建成年份)
BF7 = 当 地下室1区 未缺失时
BF10 = max(0, 1696 - 地下室1区) * BF7
BF11 = 当 质量 为 1, 8 时
BF13 = 当 类型 为 90, 150, 160, 180, 190 时
BF15 = 当 邻里 为 北岭, 北岭高地, 地标, 克劳福德, 蓝调, 林地, 绿山, 清溪, 萨默塞特村, 石桥, 维恩克 时
BF17 = 当 地下室总面积 未缺失时
BF19 = max(0, 地下室总面积 - 1392) * BF17
BF21 = max(0, 一楼面积 - 2402)
BF23 = 当 条件 为 1, 2, 3, 4, 5, 6 时
BF25 = 当 质量 为 1, 7, 10 时
BF27 = max(0, 一楼面积 - 2207)
BF30 = max(0, 15138 - 地段区域)
销售价格 = 325577 - 57.6167 * BF2 + 115438 * BF3 - 605.079 * BF6 - 25.3989 * BF10 - 66735.2 *
BF11 - 23688.9 * BF13 + 22374.5 * BF15 + 50.3801 * BF19 - 576.789 * BF21 - 18099.2 * BF23 +
22414.2 * BF25 + 361.254 * BF27 - 1.82 * BF30
关键结果:回归方程
在这些结果中,BF2 在回归方程中具有负系数。基函数的系数为 −57.6167。基函数的排列为 最大值(0, c - X)。在这种安排中,基函数的值随着预测变量的增加而减小。这种安排和负系数的组合在预测变量和响应变量之间创建了正关系。从 生活区 438 到 3,078 的斜率为 57.6167。
有关常见基函数的更多示例,请转到 的回归方程 MARS® 回归。
