注意
此命令适用于 预测分析模块。单击此处了解更多关于如何激活模块的信息。
y = b0 + b1BF1 + b2BF2 +...+ bkBFk
- y 是响应变量
- b0 是常数项
- b1 + b2 + ...+ bk 是基函数的系数
- BF1 + BF2 + ...+ BFk 是基函数
求解预测变量值的基函数以计算响应的预测值。
基函数
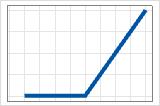
- 最大值(0, X − c)
- 正系数
- 贡献为 0 直到 c,然后增加。
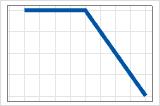
- 最大值(0, X − c)
- 负系数
- 贡献是最大值,直到 c,然后减少。
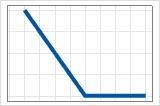
- 最大值(0, c − X)
- 正系数
- 贡献从最大值开始,逐渐减少,直到 c。在 c 之后,贡献为 0。
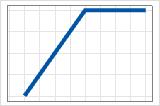
- 最大值(0, c − X)
- 负系数
- 贡献从 0 开始,一直增加到 c。在 c 之后,贡献处于最大值。
如果 c 等于预测变量的最小值或最大值,则预测变量对基函数的所有值具有相同的效应。这 2 种情况的部分依赖图显示了一条直线。MARS® 回归 使 c 成为不允许预测变量转换的分析中的端点之一。
对于类别预测变量,基函数是指标函数。该函数对于某些类别的值为 0,对于其他类别的值为 1。基函数具有以下形式:
当 X 为x1时,...xk, 其中 k 是基函数中的水平数,k ≥ 1。
对于基函数中的类别,函数的值为 1。将基函数乘以回归方程中的系数可确定函数从 0 变为 1 时的效果。
1 基函数中的连续预测变量示例
在这些结果中,BF2 在回归方程中具有负系数。基函数的系数为 −57.6167。基函数的排列为 最大值(0, c − X)。在这种安排中,基函数的值随着预测变量的增加而减小。这种安排和负系数的组合在预测变量和响应变量之间创建了正关系。其 生活区 效果是该地区的效果从 销售价格 438增加到3,078。从 生活区 438 到 3,078 的斜率为 57.6167。
回归方程
BF3 = 当 质量 为 8, 9, 10 时
BF6 = max(0, 2002 - 建成年份)
BF7 = 当 地下室1区 未缺失时
BF10 = max(0, 1696 - 地下室1区) * BF7
BF11 = 当 质量 为 1, 8 时
BF13 = 当 类型 为 90, 150, 160, 180, 190 时
BF15 = 当 邻里 为 北岭, 北岭高地, 地标, 克劳福德, 蓝调, 林地, 绿山, 清溪, 萨默塞特村, 石桥, 维恩克 时
BF17 = 当 地下室总面积 未缺失时
BF19 = max(0, 地下室总面积 - 1392) * BF17
BF21 = max(0, 一楼面积 - 2402)
BF23 = 当 条件 为 1, 2, 3, 4, 5, 6 时
BF25 = 当 质量 为 1, 7, 10 时
BF27 = max(0, 一楼面积 - 2207)
BF30 = max(0, 15138 - 地段区域)
销售价格 = 325577 - 57.6167 * BF2 + 115438 * BF3 - 605.079 * BF6 - 25.3989 * BF10 - 66735.2 *
BF11 - 23688.9 * BF13 + 22374.5 * BF15 + 50.3801 * BF19 - 576.789 * BF21 - 18099.2 * BF23 +
22414.2 * BF25 + 361.254 * BF27 - 1.82 * BF30
一个预测变量部分依赖图
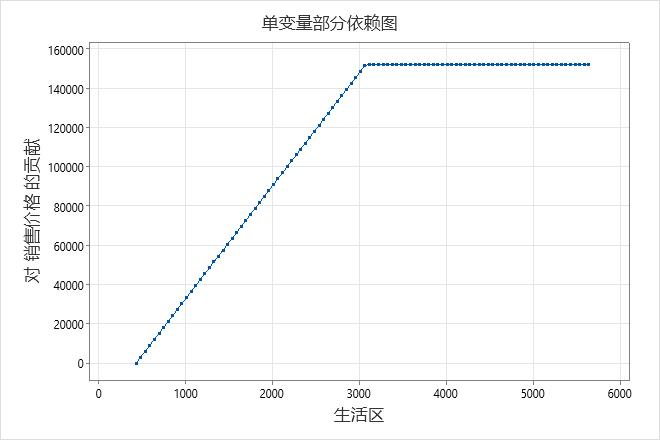
在加性模型中,使用单预测变量部分依赖图来深入了解重要的连续预测变量如何影响预测响应。一个预测变量偏相关性图指示预期响应如何随预测变量水平的变化而变化。对于 MARS® 回归,图上的值来自 x 轴上预测变量的基础函数。y 轴上的贡献是标准化的,因此图上的最小值为 0。
该图说明了随着 销售价格 数据集中最小平方英尺增加到约 3,000 平方英尺而 生活区 增加。在达到3,000平方英尺后 生活区 ,捐款 销售价格 将保持不变,约为152,000美元。
1 基函数中的类别预测变量示例
在这些结果中,BF3 用于预测变量 质量。当 的值 质量 为 8、9 或 10 时,基函数适用于。方程中BF3的系数为115,438。此基函数指示当质量值从 1 到 7 的值更改为 8、9 或 10 的值时,模型中的销售价格将增加 115,438 美元。质量 也在BF11和BF25中。要了解预测变量对响应变量的影响,请考虑所有基函数。
回归方程
BF3 = 当 质量 为 8, 9, 10 时
BF6 = max(0, 2002 - 建成年份)
BF7 = 当 地下室1区 未缺失时
BF10 = max(0, 1696 - 地下室1区) * BF7
BF11 = 当 质量 为 1, 8 时
BF13 = 当 类型 为 90, 150, 160, 180, 190 时
BF15 = 当 邻里 为 北岭, 北岭高地, 地标, 克劳福德, 蓝调, 林地, 绿山, 清溪, 萨默塞特村, 石桥, 维恩克 时
BF17 = 当 地下室总面积 未缺失时
BF19 = max(0, 地下室总面积 - 1392) * BF17
BF21 = max(0, 一楼面积 - 2402)
BF23 = 当 条件 为 1, 2, 3, 4, 5, 6 时
BF25 = 当 质量 为 1, 7, 10 时
BF27 = max(0, 一楼面积 - 2207)
BF30 = max(0, 15138 - 地段区域)
销售价格 = 325577 - 57.6167 * BF2 + 115438 * BF3 - 605.079 * BF6 - 25.3989 * BF10 - 66735.2 *
BF11 - 23688.9 * BF13 + 22374.5 * BF15 + 50.3801 * BF19 - 576.789 * BF21 - 18099.2 * BF23 +
22414.2 * BF25 + 361.254 * BF27 - 1.82 * BF30
注意
在传统的回归方程中,回归方程中的系数始终表示从 0 到 1 的变化。在 中 MARS® 回归,系数可以表示从 1 到 0 的变化。考虑一个二元分类变量,当患者报告他们没有头痛时,该变量为 0,当患者报告他们头痛时为 1。假设预测变量具有以下基函数:
- BF1 = 当头痛为 0 时
1 个预测变量的多个基函数
MARS® 回归 对单个预测变量使用多个基函数来对预测变量和响应变量之间更复杂的非线性关系进行建模。附加基函数在预测变量和响应变量之间关系的斜率中创建附加变化。MARS® 回归 允许加性模型中多个基函数中的预测变量。
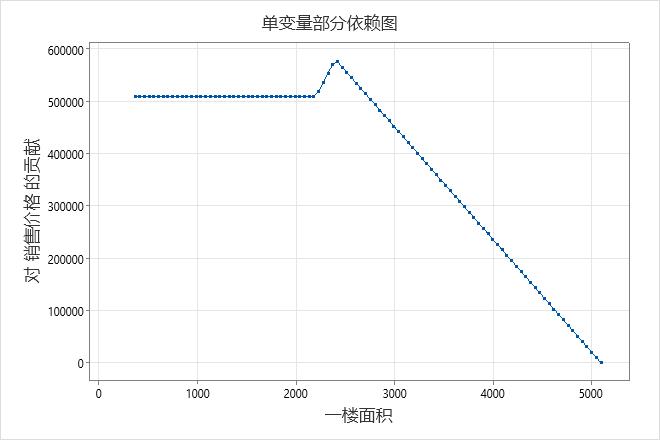
在这些结果中,BF21 用于预测变量 一楼面积。基函数 BF27 也适用于 一楼面积。BF21 和 BF27 都有相同的排列方式,最大值(0, X − c)。当预测变量的值大于 c 时,此排列中的基函数会影响响应变量。对于具有此排列的 2 个基函数,在预测变量达到 1 个基函数中的最小值之前,两个基函数都不会影响响应。在这些结果中,BF27 中的该值为 2,207。一楼面积 从最小值到 2,207 的斜率为 0。在 2,207 之后,适用 BF27 的斜率,导致斜率为 361.254。该斜率一直持续到预测变量达到 BF21 中的常数,此时 BF27 和 BF21 的系数都会产生影响 销售价格。两个系数的总和得到新的斜率,361.254 + (−576.789) = −215.535。在加性模型中, MARS® 回归 显示单预测变量的部分依赖图以显示预测变量的效果。
回归方程
BF3 = 当 质量 为 8, 9, 10 时
BF6 = max(0, 2002 - 建成年份)
BF7 = 当 地下室1区 未缺失时
BF10 = max(0, 1696 - 地下室1区) * BF7
BF11 = 当 质量 为 1, 8 时
BF13 = 当 类型 为 90, 150, 160, 180, 190 时
BF15 = 当 邻里 为 北岭, 北岭高地, 地标, 克劳福德, 蓝调, 林地, 绿山, 清溪, 萨默塞特村, 石桥, 维恩克 时
BF17 = 当 地下室总面积 未缺失时
BF19 = max(0, 地下室总面积 - 1392) * BF17
BF21 = max(0, 一楼面积 - 2402)
BF23 = 当 条件 为 1, 2, 3, 4, 5, 6 时
BF25 = 当 质量 为 1, 7, 10 时
BF27 = max(0, 一楼面积 - 2207)
BF30 = max(0, 15138 - 地段区域)
销售价格 = 325577 - 57.6167 * BF2 + 115438 * BF3 - 605.079 * BF6 - 25.3989 * BF10 - 66735.2 *
BF11 - 23688.9 * BF13 + 22374.5 * BF15 + 50.3801 * BF19 - 576.789 * BF21 - 18099.2 * BF23 +
22414.2 * BF25 + 361.254 * BF27 - 1.82 * BF30
缺失值的基础函数
在搜索基函数时, MARS® 回归 为任何具有缺失值的预测变量创建指示变量。指示符变量显示是否缺少预测变量的值。如果分析包括模型中具有缺失值的预测变量的基础函数,则模型还包括指示变量的基础函数。预测变量的其他基函数都与指示变量的基函数交互。
当预测变量具有缺失值时,指示变量的基础函数通过乘以 0 使该预测变量的其他基础函数无效。缺失值的这些基函数存在于重要预测变量具有缺失值的所有模型中,甚至是加法模型和禁用其他类型的变换的模型。
在这些结果中,BF7 用于预测变量 地下室1区。当在数据中时 地下室1区 ,BF 7 的值为 1。缺少 BF 7 时 地下室1区 的值为 0。回归方程中不存在BF7,因为基函数在最终模型中并不重要,但BF7与BF10相互作用。BF10很重要,存在于回归方程中。BF7 的效果是在缺失时地下室1区将 BF10 乘以 0,从而消除缺失时 地下室1区 的效果。
回归方程
BF3 = 当 质量 为 8, 9, 10 时
BF6 = max(0, 2002 - 建成年份)
BF7 = 当 地下室1区 未缺失时
BF10 = max(0, 1696 - 地下室1区) * BF7
BF11 = 当 质量 为 1, 8 时
BF13 = 当 类型 为 90, 150, 160, 180, 190 时
BF15 = 当 邻里 为 北岭, 北岭高地, 地标, 克劳福德, 蓝调, 林地, 绿山, 清溪, 萨默塞特村, 石桥, 维恩克 时
BF17 = 当 地下室总面积 未缺失时
BF19 = max(0, 地下室总面积 - 1392) * BF17
BF21 = max(0, 一楼面积 - 2402)
BF23 = 当 条件 为 1, 2, 3, 4, 5, 6 时
BF25 = 当 质量 为 1, 7, 10 时
BF27 = max(0, 一楼面积 - 2207)
BF30 = max(0, 15138 - 地段区域)
销售价格 = 325577 - 57.6167 * BF2 + 115438 * BF3 - 605.079 * BF6 - 25.3989 * BF10 - 66735.2 *
BF11 - 23688.9 * BF13 + 22374.5 * BF15 + 50.3801 * BF19 - 576.789 * BF21 - 18099.2 * BF23 +
22414.2 * BF25 + 361.254 * BF27 - 1.82 * BF30
交互的基础函数
为了对交互作用进行建模, MARS® 回归 请将不同预测变量的基础函数相乘。MARS® 回归 不考虑默认加法模型中的交互作用。部分依赖图不适用于考虑交互作用的分析。
交互作用意味着预测变量的效应取决于其他预测变量的值。例如,谷物在烤箱中的干燥速度取决于烤箱中的时间,但时间的影响取决于烤箱的温度。时间和温度变量相互作用。
在具有交互作用的模型的结果中,BF9 用于预测变量 质量。BF12 用于预测变量 一楼面积。BF12 的计算包括乘以 BF9,因此两个预测变量相互作用。确定 质量 效应或 一楼面积 需要了解其他预测变量的值。BF12 的系数 −63.1685 仅在 BF9 的值为 1 时适用。当 8、9 或 10 时,BF9 的值为 1 质量 。由于 BF12 的排列,当平方英尺小于 2, 一楼面积 470 且值 质量 为 8、9 或 10 时,斜率为 63.1685。
回归方程
BF4 = max(0, 2002 - 建成年份)
BF5 = 当 地下室1区 未缺失时
BF7 = max(0, 地下室1区 - 1758) * BF5
BF8 = max(0, 1758 - 地下室1区) * BF5
BF9 = 当 质量 为 8, 9, 10 时
BF12 = max(0, 2470 - 一楼面积) * BF9
BF14 = 当 质量 为 7, 9, 10 时
BF15 = 当 类型 为 75, 90, 150, 160, 180, 190 时
BF19 = 当 邻里 为 北岭, 北岭高地, 克劳福德, 蓝调, 林地, 绿色, 绿山, 清溪, 萨默塞特村, 石桥, 维恩克 时 * BF5
BF21 = 当 条件 为 1, 2, 3, 4, 5, 6 时 * BF4
BF25 = max(0, 一楼面积 - 372) * BF7
BF26 = 当 地下室总面积 未缺失时 * BF14
BF28 = max(0, 地下室总面积 - 689) * BF26
销售价格 = 320349 - 66.4387 * BF2 - 28.2065 * BF8 + 123645 * BF9 - 63.1685 * BF12 - 23751.7 *
BF15 + 22818.2 * BF19 - 523.924 * BF21 - 0.036887 * BF25 + 53.9878 * BF28
