注意
此命令适用于 预测分析模块。单击此处了解更多关于如何激活模块的信息。
一组研究人员从位于爱荷华州艾姆斯的个人住宅物业的出售中收集数据。研究人员希望找出影响销售价格的变量。变量包括住宅物业的地块大小和各种功能。研究人员希望评估最佳MARS® 模型与数据的拟合程度。
- 打开样本数据 艾姆斯住房.MWX。
- 选择 。
- 在响应中,输入“销售价格”。
- 在 中 连续预测变量,输入’地段正面’ – ‘销售年份’。
- 在 中 类别预测变量,输入 类型 – '销售条件'。
- 单击 确定。
解释结果
默认情况下, 拟合加性模型, MARS® 回归 因此回归方程中的所有基函数都使用 1 个预测变量。列表中的第一个预测变量是 BF2。BF2 使用预测变量 生活区。由于预测变量位于 1 个基函数中,因此预测变量在模型中具有 2 个不同的斜率。函数 max(0, 3078 - 生活区) 定义当居住面积小于 3,078 时斜率不为零。
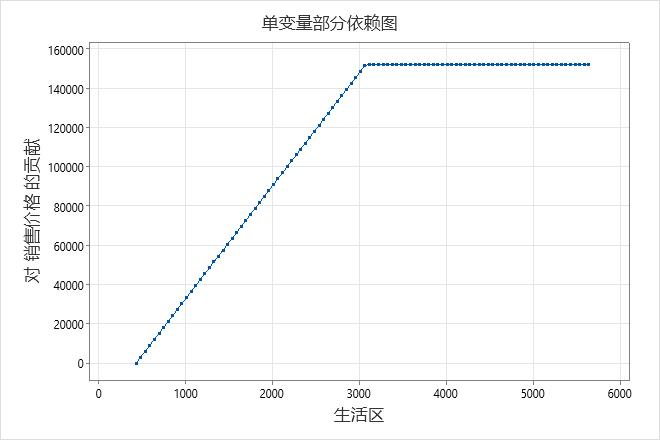
加性模型的结果包括模型中重要的连续预测变量的部分依赖图。使用该图可以查看预测变量在预测变量范围内的所有基函数的效应。在这些结果中,部分依赖图显示,对于从 438 到 3,078 的值 生活区 ,斜率约为 57.6。当大于 3,078 时 生活区 ,斜率为 0。
在这些结果中,BF2 在回归方程中具有负系数。基函数的排列为 最大值(0, c - X)。在这种安排中,基函数的值随着预测变量的增加而减小。这种安排和负系数的组合在预测变量和响应变量之间创建了正关系。其 生活区 效果是该地区的效果从 销售价格 438增加到3,078。
分析还包括类别预测变量。例如,BF3 用于预测变量 质量。当 的值 质量 为 8、9 或 10 时,基函数适用于。方程中BF3的系数为115,438。此基函数指示当质量值从 1 到 7 的值更改为 8、9 或 10 的值时,模型中的销售价格将增加 115,438 美元。质量 也在BF11和BF25中。要了解预测变量对响应变量的影响,请考虑所有基函数。
模型中重要的两个预测变量在训练数据中缺少值:地下室1区 和 地下室总面积.基函数列表包括用于标识何时缺少这些预测变量的基函数:BF7 和 BF17。当预测变量具有缺失值时,指示变量的基础函数通过乘以 0 使该预测变量的其他基础函数无效。
回归方程
BF3 = 当 质量 为 8, 9, 10 时
BF6 = max(0, 2002 - 建成年份)
BF7 = 当 地下室1区 未缺失时
BF10 = max(0, 1696 - 地下室1区) * BF7
BF11 = 当 质量 为 1, 8 时
BF13 = 当 类型 为 90, 150, 160, 180, 190 时
BF15 = 当 邻里 为 北岭, 北岭高地, 地标, 克劳福德, 蓝调, 林地, 绿山, 清溪, 萨默塞特村, 石桥, 维恩克 时
BF17 = 当 地下室总面积 未缺失时
BF19 = max(0, 地下室总面积 - 1392) * BF17
BF21 = max(0, 一楼面积 - 2402)
BF23 = 当 条件 为 1, 2, 3, 4, 5, 6 时
BF25 = 当 质量 为 1, 7, 10 时
BF27 = max(0, 一楼面积 - 2207)
BF30 = max(0, 15138 - 地段区域)
销售价格 = 325577 - 57.6167 * BF2 + 115438 * BF3 - 605.079 * BF6 - 25.3989 * BF10 - 66735.2 *
BF11 - 23688.9 * BF13 + 22374.5 * BF15 + 50.3801 * BF19 - 576.789 * BF21 - 18099.2 * BF23 +
22414.2 * BF25 + 361.254 * BF27 - 1.82 * BF30
注意
在这些结果中,基函数列表有 15 个基函数,但最佳基函数数为 13。回归方程包含 13 个基函数。基函数列表包含 BF7 和 BF17,它们是标识缺失值的基础函数。这些基函数本身并不重要,因为它们在搜索中没有像其他基函数那样减少MSE。这两个基函数在列表中显示了 BF10 和 BF 19 的完整计算,这很重要。
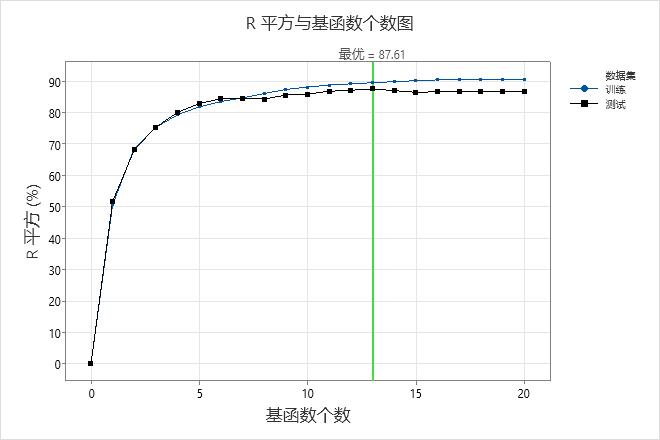
R 平方与基函数数图显示了向后消除的结果,以找到最佳基函数数。要使用具有不同基函数数的模型,请选择 选择备择模型。例如,如果基函数少得多的模型几乎与最优模型一样准确,请考虑是否使用更简单的模型。在这些结果中,训练数据集和测试数据集的 R 平方值对于具有 7 个基函数的模型相同。如果过度拟合是一个问题,这个较小的模型会很有趣。
模型汇总
| 总预测变量 | 77 |
|---|---|
| 重要预测变量 | 10 |
| 基函数的最大数量 | 30 |
| 基函数的最优数量 | 13 |
| 统计量 | 训练 | 测试 |
|---|---|---|
| R 平方 | 89.61% | 87.61% |
| 均方根误差 (RMSE) | 25836.5197 | 27855.6550 |
| 均方误差 (MSE) | 667525749.7185 | 775937512.8264 |
| 平均绝对偏差 (MAD) | 17506.0038 | 17783.5549 |
模型摘要表包括模型性能的度量。您可以使用这些值来比较模型。对于这些结果,检验 R 平方约为 88%。
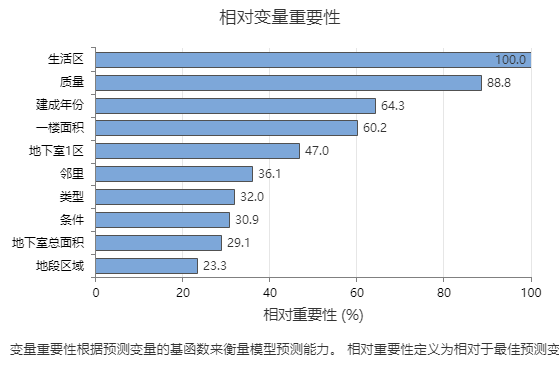
相对变量重要性图按预测变量对模型的影响顺序绘制预测变量。最重要的预测变量是 生活区。如果顶部预测变量 生活区的贡献为 100%下一个重要变量 质量的贡献为 88.8%。这个贡献意味着它 质量 的重要性 生活区 是这个模型的88.8%。
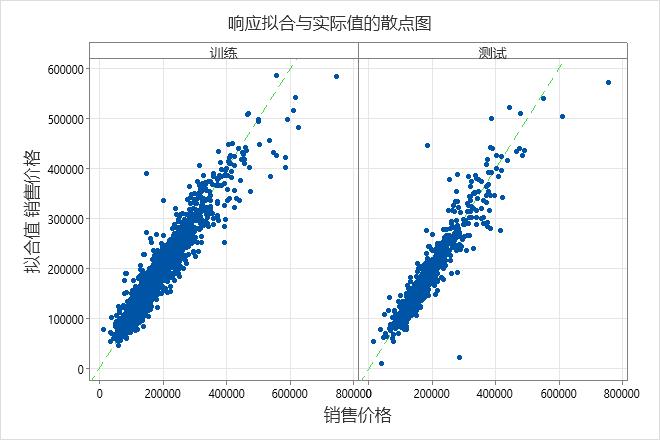
拟合销售价格与实际销售价格的散点图显示了训练数据和检验数据的拟合值和实际值之间的关系。您可以将鼠标悬停在图形上的点上,以便更轻松地查看标绘的值。在此示例中,大多数点大约落在 y=x 的参考线附近。
该模型对几个不同点的拟合很差,例如测试数据集中的拟合销售价格低于 100,000 美元但实际销售价格接近 250,000 美元的模型。考虑是否调查此案例以提高模型的拟合度。
