步骤 1:调查备择树
R 平方与终端节点数图显示每个树的 R2 值。默认情况下,初始回归树是 R2 值在最大 R2 值的树的 1 个标准误内的最小树。当分析使用交叉验证或检验数据集时,R2 值来自于验证样本。验证样本的值通常趋于平稳,并最终随着树变大而开始下降。
单击选择备择树可打开包含模型汇总统计量表的交互图。可使用该图调查性能相似的备择树。
- Minitab 选择的树属于标准改进的模式。具有更多个节点的一个或多个树属于同一模式。通常,您希望从树进行预测,并尽可能地提高预测准确度。
- Minitab 选择的树属于标准相对平直的模式。与最优树相比,模型汇总统计量相似的一个或多个树的节点要少得多。通常,树的终端节点越少,越能清晰地显示每个预测变量如何影响响应值。较小的树也更易于识别一些目标组,以便进一步研究。如果较小树的预测准确度差异可以忽略不计,则也可以使用较小的树来评估响应变量与预测变量之间的关系。
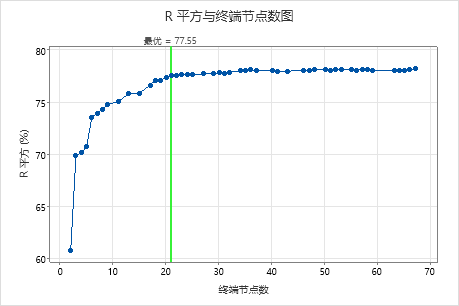
关键结果:具有 21 个终端节点的树的 R 平方与终端节点数图
具有 21 个终端节点的回归树的 R2 值约为 0.78。此树的标签为“最优”,因为树的创建标准是 R2 值在最大 R2 值 1 个标准误内的最小树。由于此图显示具有约 20 个节点的树和具有约 70 个节点的树之间的 R2 值相对稳定,因此研究人员希望查看与结果中的树类似、但更小的一些树的性能。比较下一个图形,查看具有 17 个节点的树的结果。
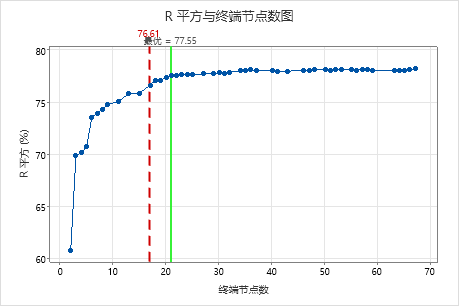
关键结果:具有 17 个终端节点的树的 R 平方与终端节点数图
具有 17 个终端节点的回归树的 R2 值为 0.7661。使用选择备择树为不同的树创建结果时,来自初始结果的树会保留“最优”标签。
步骤 2:调查树状图上值得关注的节点
选择树后,可以调查树状图上独特的终端节点。例如,您可能关注均值较大或标准差较小的节点。从详细视图中,您可以看到每个节点的均值、标准差和总计数。
注意
右键单击树状图可执行以下交互:
- 突出显示从节点拟合值变异最小的 5 个节点。这些节点为最优节点。
- 根据树的标准,突出显示 5 个均值或中位数最高的节点。
- 根据树的标准,突出显示 5 个均值或中位数最低的节点。
- 复制产生所选节点的预测变量的值。这些值是节点规则。
- 显示节点分裂视图。当您有一个大型树并且只想查看哪些变量分裂节点时,此视图非常有用。
节点继续分裂,直到终端节点无法再为了进一步分组而进行分裂。探索其他节点,看看哪些变量最值得关注。
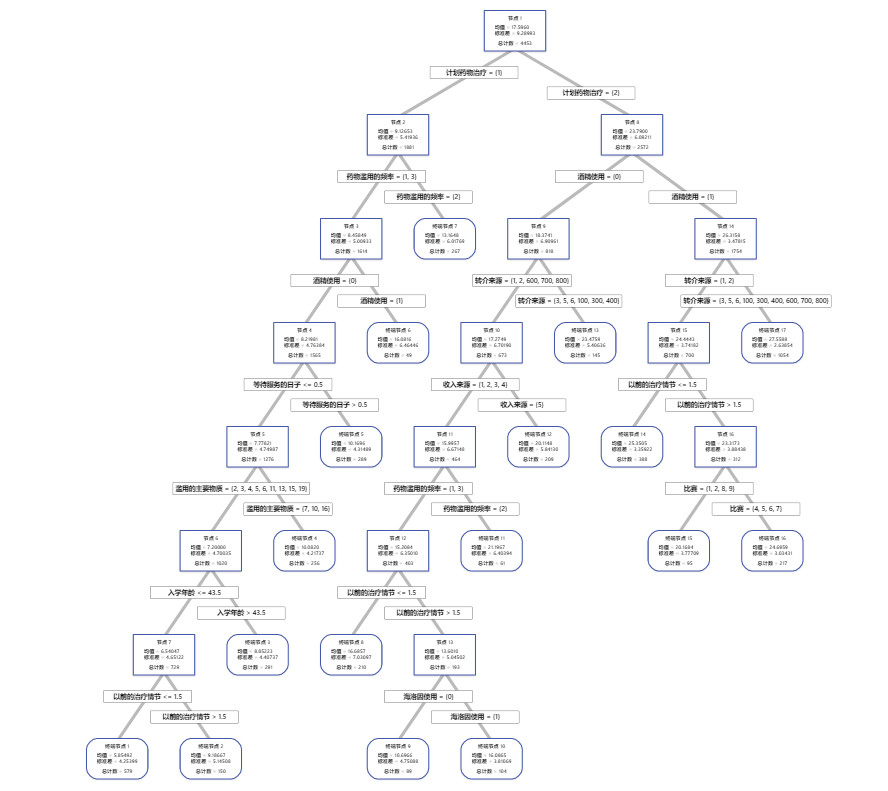
关键结果:具有 17 个节点的树状图
树状图显示完整数据集中的全部 4453 个案例。您可以在详细视图和节点分裂视图之间切换树的视图。
- 节点 2 具有计划药物治疗 = 1 的案例。此节点有 1881 个案例。该节点的均值小于整体均值。节点 2 的标准差约为 5.4,小于整体标准差,因为分裂会产生更纯的节点。
- 节点 8 具有计划药物治疗 = 2 的案例。此节点有 2572 个案例。该节点的均值大于整体均值。节点 8 的标准差约为 6.1,也小于整体标准差。
然后,节点 2 按药物滥用的频率分裂,节点 8 按酒精使用分裂。终端节点 17 具有计划药物治疗 = 2、酒精使用 = 1 和转介来源 = 3、5、6、100、300、400、600、700 或 800 的案例。研究人员指出,终端节点 17 具有最高的均值、最小的标准差和最多的案例。
终端节点 1 的均值最小,标准差约为 4.3。由于终端节点 1 的均值约为 5.9,并且响应值不能为负,因此节点统计量表明终端节点 1 中的数据可能向右偏斜。
步骤 3:确定重要变量
使用相对变量重要性图可查看哪些预测变量是树最重要的变量。
重要变量是树中的主分裂变量或代理分裂变量。改进得分最高的变量设置为最重要的变量,其他变量依次排序。相对变量重要性将重要性值标准化,以便于解释。相对重要性定义为相对于最重要预测变量的改进百分比。
相对变量重要性的值范围是 0% 到 100%。最重要变量的相对重要性始终为 100%。如果变量不在树中,则该变量就不重要。
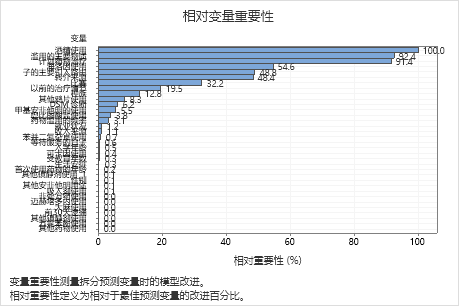
关键结果:相对变量重要性
- 滥用的主要物质和计划药物治疗的重要性约为酒精使用的 92%。
- 海洛因使用的重要性约为酒精使用的 55%。
- 子的主要引入路由和转介来源的重要性约为酒精使用的 48%。
尽管这些结果包含 33 个重要性为正的变量,但可以根据相对排名来确定针对特定应用要控制或监控多少个变量。如果相对重要性值从一个变量到下一个变量存在大幅下降,则可以据此决定要控制或监控哪些变量。例如,在这些数据中,有三个最重要变量,它们的重要性值相对接近,随后下一个变量的相对重要性则下降近 40%。同样,有三个变量的重要性值相似,接近 50%。您可以从不同的组中删除变量并重做分析,以评估各个组中的变量如何影响模型汇总表中的预测准确度值。
