某医疗保健提供商运营着一家提供吸毒治疗服务的机构。该机构的其中一项服务是门诊戒毒计划,其常规治疗疗程可持续 1 至 30 天。负责预测人员配备和物品供应的团队希望研究,他们是否可以根据患者加入计划时可以收集的患者相关信息,对患者使用服务的时长做出更好的预测。这些变量包括人口统计信息和有关患者吸毒的变量。
首先,团队在 Minitab 中考虑采用传统的回归分析。由于数据中存在缺失值模式,因此分析省略了 70% 以上的数据。忽略如此大的数据比例意味着大量信息丢失。没有任何缺失数据的案例的分析结果与使用整个数据集的结果可能大不相同。由于 CART® 回归 会自动处理预测变量中的缺失值,因此团队决定使用 CART® 回归 来进一步评估其数据。
- 打开样本数据集服务年限.MWX。
- 选择 。
- 在 响应中,输入服务年限。
- 在 连续预测变量 中,输入 入学年龄-受教育年数。
- 在 类别预测变量 中,输入 其他兴奋剂使用-'DSM 诊断'。
- 单击 验证。
- 在验证方法中,选择 K 折叠交叉验证。
- 选择 按 ID 列分配每个折叠的行。
- 在 ID 列中,输入倍。
- 单击每个对话框中的确定。
解释结果
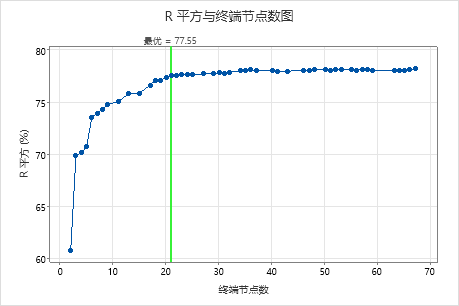
默认情况下,Minitab 显示 R2 值在 R2 值最大的树的 1 个标准误内的最小树。由于医疗团队使用 k 折叠验证,因此标准是最大 k 折叠 R2 值。此树有 21 个终端节点。
选择备择树
- 在输出中,单击选择备择树
- 在图中,选择 17 节点树。
- 单击 创建树。
解释结果
研究人员查看交叉验证的 R2 统计量和终端节点数的绘图。由于具有 17 个节点的树的 R2 统计量接近图上的最大值,因此其余输出的结果适用于具有 17 个节点的树。
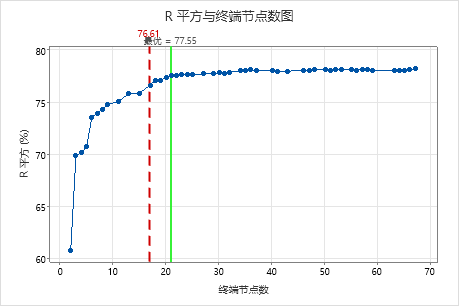
研究人员首先查看模型汇总,以评估较小树的性能。训练和检验统计量的值非常接近,因此树看起来不会过度拟合。R2 统计量几乎与 21 节点树一样高,因此研究人员决定使用具有 17 个节点的树来探索预测变量和响应值之间的关系。
方法
| 节点分裂 | 最小平方误差 |
|---|---|
| 最优树 | 最大 R 平方的 2.5 个标准误内 |
| 模型验证 | 由 倍 定义的行的交叉验证 |
| 已使用的行数 | 4453 |
响应信息
| 均值 | 标准差 | 最小值 | 下四分位数 | 中位数 | 上四分位数 | 最大值 |
|---|---|---|---|---|---|---|
| 17.5960 | 9.29097 | 1 | 10 | 18 | 26 | 30 |
模型汇总
| 总预测变量 | 44 |
|---|---|
| 重要预测变量 | 33 |
| 终端节点数 | 17 |
| 最小终端节点大小 | 49 |
| 统计量 | 训练 | 测试 |
|---|---|---|
| R 平方 | 77.99% | 76.61% |
| 均方根误差 (RMSE) | 4.3585 | 4.4932 |
| 均方误差 (MSE) | 18.9967 | 20.1887 |
| 平均绝对偏差 (MAD) | 3.4070 | 3.5226 |
| 平均绝对百分比误差 (MAPE) | 0.6535 | 0.6674 |
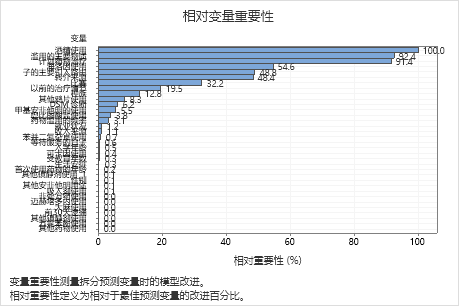
- 滥用的主要物质 并且 计划药物治疗 大约 酒精使用92% 的重要性与 .
- 海洛因使用 的重要性约为 酒精使用的 55%。
- 子的主要引入路由 并且 转介来源 大约 酒精使用48% 的重要性与 .
尽管这些结果包含 33 个重要性为正的变量,但可以根据相对排名来确定针对特定应用要控制或监控多少个变量。如果相对重要性值从一个变量到下一个变量存在大幅下降,则可以据此决定要控制或监控哪些变量。例如,在这些数据中,有三个最重要变量,它们的重要性值相对接近,随后下一个变量的相对重要性则下降近 40%。同样,三个变量的重要性值接近 50%。您可以从不同的组中删除变量并重做分析,以评估各个组中的变量如何影响模型汇总表中的预测准确度值。
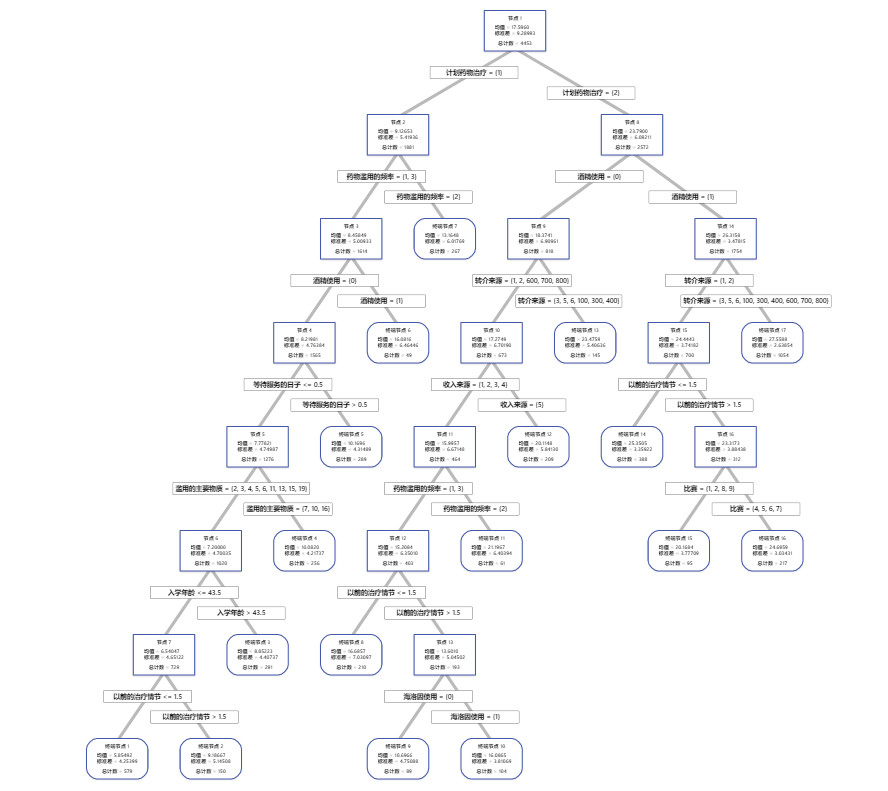
对于使用 k 折叠交叉验证的分析,树状图显示完整数据集中的全部 4453 个案例。您可以在详细视图和节点分裂视图之间切换树的视图。拟合和误差统计量表以及对象分类标准提供了有关终端节点的其他信息。
- 节点 2 包括 计划药物治疗 = 1 的案例。此节点有 1881 个案例。该节点的均值小于整体均值。节点 2 的标准差约为 5.4,小于整体标准差,因为分裂会产生更纯的节点。
- 节点 8 包括 计划药物治疗 = 2 的案例。此节点有 2572 个案例。该节点的均值大于整体均值。节点 8 的标准差约为 6.1,也小于整体标准差。
然后,节点 2 按 药物滥用的频率 分裂,节点 8 按 酒精使用 分裂。终端节点 17 具有 计划药物治疗 = 2、酒精使用 = 1 和 转介来源 = 3、5、6、100、300、400、600、700 或 800 的案例。研究人员指出,终端节点 17 具有最高的均值、最小的标准差和最多的案例。
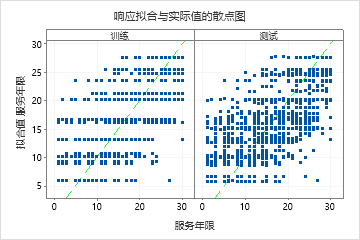
结果包括拟合响应值和实际响应值的散点图。用于训练数据集和检验数据集的点显示了相似的模式。这种相似性表明树在新数据上的性能接近于树在训练数据上的性能。
- 计划药物治疗 = {2}
- 酒精使用 = {0}
- 转介来源 = {1, 2, 600, 700, 800}
- 收入来源 = {1, 2, 3, 4}
- 药物滥用的频率 = {1, 3}
- 以前的治疗情节 <= 1.5
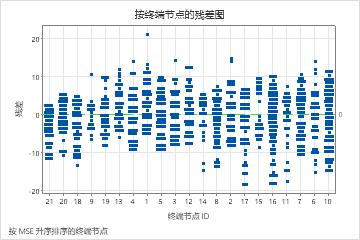
按终端节点的残差图显示:在终端节点 8 中,拟合对于一小群患者来说过大。分析人员想要调查为什么其中一些患者使用服务的时间短于他们组中的典型患者。例如,如果这些患者与终端节点中其他患者位于不同的地理位置,则不同的政府和保险法规可能会影响他们使用服务的时长。
按终端节点的残差图显示了分析人员可以选择调查聚类或异常值的其他案例。例如,在这些数据中,有一个残差比终端节点 1 和终端节点 7 中的其他残差大得多。分析人员决定调查这些患者使用服务的时间长于该终端节点上其他患者的原因。
由于检验 R2 值还有改进空间,并且残差图显示了树拟合不佳的案例,因此研究人员考虑是使用 TreeNet® 回归 还是 Random Forests® 回归 来尝试改善拟合度。