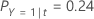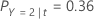分类树是对原始训练数据集进行二叉树递归分割的结果。树中的任何父节点(训练数据的子集)都可通过有限数量的方式分裂为两个互斥的子节点,具体取决于在节点中收集的实际数据值。
分裂过程将预测变量视为连续变量或类别变量。对于连续变量 X 和值 c,分裂是通过将 X 的值小于或等于 c 的所有记录发送到左侧节点,将剩余的所有记录发送到右侧节点来定义的。CART 始终使用两个相邻值的平均值来计算 c。具有 N 个可区分值的连续变量将生成最多 N–1 个父节点的潜在分裂(当施加最小允许节点大小限制时,实际数量将会更少)。
例如,连续预测变量具有数据中的值 55、66 和 75。此变量的一个可能分裂是将所有小于或等于 (55+66)/2 = 60.5 的值发送到一个子节点,将所有大于 60.5 的值发送到另一个子节点。预测变量值为 55 的案例转到一个节点,值为 66 和 75 的案例转到另一个节点。此预测变量的另一个可能分裂是将所有小于或等于 70.5 的值发送到一个子节点,将大于 70.5 的值发送到另一个节点。值为 55 和 66 的案例转到一个节点,值为 75 的案例转到另一个节点。
对于具有可区分值 {c1, c2, …, ck} 的类别变量 X,分裂被定义为发送到左侧子节点的水平子集。具有 K 个水平的类别变量最多生成 2K-1–1 个分裂。
| 左侧子节点 | 右侧子节点 |
|---|---|
| 红色、蓝色 | 黄色 |
| 红色、黄色 | 蓝色 |
| 蓝色、黄色 | 红色 |
在分类树中,目标是具有 K 个可区分类别的多项式。树的主要目标是找到一种方法,以尽可能纯的方式将不同的目标类别分离到单独的节点中。生成的终端节点数无需为 K;可使用多个终端节点来表示特定的目标类别。用户可以指定目标类别的先验概率;CART 将在树增长过程中将其考虑在内。
在以下部分中,Minitab 对二值响应变量使用以下定义:
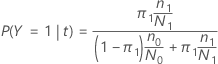
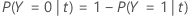
在以下部分中,Minitab 对多项式响应变量使用以下定义:
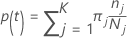
节点 t 中类别 j 的概率:
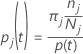
这些定义给出了节点内的概率。Minitab 会为任何节点和任何潜在分裂计算这些概率。Minitab 使用以下标准之一从这些概率计算潜在分裂的整体改进。
表示法
| 项 | 说明 |
|---|---|
| K | 响应变量中的类别数 |
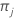 | 类别 j 的先验概率 |
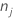 | 节点 N 中类别 j |
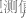 | 数据中类别 j 的观测值数 |
基尼标准
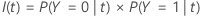
下面更通用的公式适用于多项式响应变量:
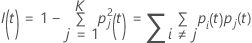
请注意,如果节点的所有观测值都在一个类别中,则  。
。
熵标准

下面更通用的公式适用于多项式响应变量:
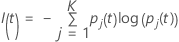
请注意,如果节点的所有观测值都在一个类别中,则  。
。
二分标准
| 超类别 1 | 超类别 2 |
|---|---|
| 1、2、3 | 4 |
| 1、2、3 | 3 |
| 1、3、4 | 2 |
| 2、3、4 | 1 |
| 1、2 | 3、4 |
| 1、3 | 2、4 |
| 1、4 | 2、3 |
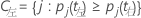
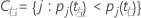
左超类别具有所有倾向于向左的目标类别。右超类别具有所有倾向于向右的目标类别。
| 类别 | 左侧子节点概率 | 右侧子节点概率 |
|---|---|---|
| 1 | 0.67 | 0.33 |
| 2 | 0.82 | 0.18 |
| 3 | 0.23 | 0.77 |
| 4 | 0.89 | 0.11 |
那么,形成候选分裂超类别的最优方式是将 {1, 2, 4} 指定为一个超类别,将 {3} 指定为另一个超类别。
计算的其余部分与以超类别作为二值目标的基尼标准相同。
标准的改进计算
计算节点杂质后,Minitab 会计算使用预测变量分裂节点的条件概率:
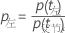
和
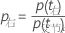
然后,从以下公式计算分裂改进:
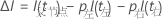
具有最高改进值的拆分成为树的一部分。如果两个预测器的改进相同,则算法需要进行选择。选择使用一个确定性的断线方案,该方案涉及预测器在工作表中的位置、预测器的类型以及分类预测器中的类数。
类别概率
节点分裂会最大程度地提高给定节点内类别的概率。
终端节点
- 节点中的案例数达到分析的最小大小。Minitab 统计软件中的默认最小值为 3。
- 节点中的所有案例都具有相同的响应类别。
- 节点中的所有案例都具有相同的预测变量值。
终端节点的预测类别
终端节点的预测类别是将节点误分类成本降至最低的类别。误分类成本的表示取决于响应变量中的类别数。由于终端节点的预测类别来自于使用验证方法时的训练数据,因此以下所有公式都使用来自训练数据集的概率。
二值响应变量
以下方程给出了节点中的案例为事件类别的预测的误分类成本:

以下方程给出了节点中的案例为非事件类别的预测的误分类成本:

| 项 | 说明 |
|---|---|
| PY=0|t | 节点 t 中的案例属于非事件类别的条件概率 |
| C1|0 | 将非事件类别案例预测为事件类别案例的误分类成本 |
| PY=1|t | 节点 t 中的案例属于事件类别的条件概率 |
| C0|1 | 将事件类别案例预测为非事件类别案例的误分类成本 |
终端节点的预测类别是误分类成本最低的类别。
多项式响应变量

例如,考虑具有三个类别的响应变量和以下误分类成本:
| 预测类别 | |||
| 实际类别 | 1 | 2 | 3 |
| 1 | 0.0 | 4.1 | 3.2 |
| 2 | 5.6 | 0.0 | 1.1 |
| 3 | 0.4 | 0.9 | 0.0 |
然后,考虑对于节点 t,响应变量的类别具有以下概率:
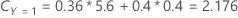


误分类成本最小的是 Y = 3, 1.164 的预测。此类别是终端节点的预测类别。