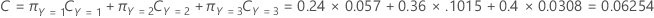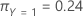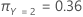当分裂方式是类别概率时,误分类表不存在。
计数
如果没有权重,则计数和样本数量相同。
加权计数
在加权情况下,加权计数是类别的权重之和。加权计数取整为最接近的整数。使用不四舍五入的权重来计算百分比和比率。请分析以下简单的示例:
| 响应水平 | 预测水平 | 权重 |
|---|---|---|
| 是 | 是 | 0.1 |
| 是 | 是 | 0.2 |
| 是 | 否 | 0.3 |
| 是 | 否 | 0.4 |
| 否 | 否 | 0.5 |
| 否 | 否 | 0.6 |
| 否 | 是 | 0.7 |
| 否 | 是 | 0.8 |
此表提供以下统计量:
| 实际类别 | 加权计数 | 分类有误 | 预测类别 = 否 | 正确数百分比 |
|---|---|---|---|---|
| 是 | 0.1 + 0.2 + 0.3 + 0.4 = 1 | 0.1 + 0.2 = 0.3 ≈ 0 | 0.3 + 0.4 = 0.7 ≈ 1 | (0.3 / 1.0) ×100 = 30% |
| 否 | 0.5 + 0.6 + 0.7 + 0.8 = 2.6 ≈ 3 | 0.7 + 0.8 = 1.5 ≈ 2 | 0.5 + 0.6 = 1.1 ≈ 1 | 1.1 / 2.6) × 100 = 42.31% |
| 全部 | 1 + 2.6 = 3.6 ≈ 4 | 0.3 + 1.5 = 1.8 ≈ 2 | 0.7 + 1.1 = 1.8 ≈ 2 | (0.3 + 1.1) / 3.6 × 100 = 38.89% |
误差百分比
在加权情况下,使用加权计数代替计数。

成本
成本的计算取决于响应变量是二值变量还是多项式变量。
成本 = (误差百分比 × 类别的输入误分类成本) / 100
二值响应变量
以下方程给出了事件类别的成本:

以下方程给出了非事件类别的成本:

以下方程给出了所有类别的总成本:

多项式响应变量
对于多项式案例,该方程扩展了二值响应变量的公式,以解释所有可能的误分类类型。例如,对于 k 类别的多项式响应,Y = 1 的误分类成本使用以下方程:
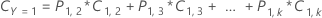
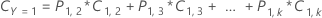
以下方程给出了多项式案例的总成本:

例如,考虑具有 3 个类别的响应变量和以下误分类成本:
| 预测类别 | |||
| 实际类别 | 1 | 2 | 3 |
| 1 | 0.0 | 4.1 | 3.2 |
| 2 | 5.6 | 0.0 | 1.1 |
| 3 | 0.4 | 0.9 | 0.0 |
然后,考虑下表给出了误差百分比:
| 预测类别 | |||
| 实际类别 | 1 | 2 | 3 |
| 1 | 暂缺 | 1% | 0.5% |
| 2 | 1.4% | 暂缺 | 2.1% |
| 3 | 5% | 1.2% | 暂缺 |
最后,考虑响应变量的类别具有以下先验概率:
以下方程给出了与响应变量中每个类别的误分类相关联的成本:






以下方程给出了总成本: