点在提升图上的过程取决于验证方法。对于多项式响应变量,Minitab 会显示多个图表,这些图表依次将每个类别视为事件。
训练数据集或无验证
对于训练数据集的图表,图表上的每个点都表示树中的一个终端节点。事件概率最高的终端节点是图表上的第一个点,显示在最左侧。其他终端节点按事件概率递减的顺序排列。
使用以下过程查找点的 x 坐标和 y 坐标。
- 计算每个终端节点的事件概率:
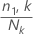
- n1,k 是第 k 个节点的事件类别中的案例数
- Nk 是第 k 个节点中的案例数
- 按事件概率从最高到最低的顺序对终端节点进行排序。
- 对于每个终端节点,将该终端节点中的案例分配给事件类别,将其他终端节点中的案例分配给非事件类。
例如,假设下表汇总了一个具有 4 个终端节点的树:
A:终端节点 B:事件数 C:案例数 D:阈值 (B/C) 4 18 30 0.60 1 25 67 0.37 3 12 56 0.21 2 4 36 0.11 合计 59 189 然后,下面是对应的真阳率,精确到小数点后 2 位:
A:终端节点 B:事件数 C:真阳率 4 18 18 / 59 = 0.31 1 25 25 / 59 = 0.42 3 12 12 / 59 = 0.20 2 4 4 / 59 = 0.07 合计 59 - 从已排序的终端节点中,查找终端节点中总体的百分比:

- Nk 是第 k 个节点中的案例数
- N 是训练数据集中的案例数
- 要查找 y 坐标的提升,将真阳率除以总体百分比:

- 对于已排序的终端节点,计算每个终端节点中数据的累积百分比。这些累积值是图表上的 x 坐标。
例如,如果预测概率最高的终端节点包含 0.16 的数据,而事件概率第二高的终端节点具有 0.35 的总体,则第一个终端节点数据的累积百分比为 0.16,第二个终端节点的总体累积百分比为 0.16 + 0.35 = 0.51。
下表显示了小树的计算示例。这些值精确到小数点后 2 位。
| A:终端节点 | B:事件数 | C:案例数 | D:排序事件概率 (B/C) | E:真阳率 | F:数据百分比(C/C 之和) | G:数据累积百分比,x 坐标 | H:提升 (E /F),y 坐标 |
|---|---|---|---|---|---|---|---|
| 4 | 18 | 30 | 0.60 | 0.31 | 0.16 | 0.16 | 1.94 |
| 1 | 25 | 67 | 0.37 | 0.42 | 0.35 | 0.51 | 1.20 |
| 3 | 12 | 56 | 0.21 | 0.20 | 0.30 | 0.81 | 0.67 |
| 2 | 4 | 36 | 0.11 | 0.07 | 0.19 | 1.00 | 0.37 |
单独的检验数据集
使用与训练数据集案例相同的步骤,但从检验数据集的案例中计算事件概率。
使用 k 折叠交叉验证进行检验
使用 k 折叠交叉验证在提升图上定义 x 和 y 坐标的过程具有额外的步骤。此步骤会创建许多可区分事件概率。例如,假设树状图包含 4 个终端节点。我们有 10 折叠交叉验证。然后,对于第 i 个折叠,您使用数据的 9/10 部分来估算折叠 i 中的案例的事件概率。当针对每个折叠重复此过程时,可区分事件概率的最大数量为 4 ^10 = 40。之后,按递减顺序对所有可区分事件概率进行排序,并对需要更多案例才能形成适当区间的任何可区分事件概率进行合并。在此步骤之后,将应用训练数据集过程从 3 到结束的步骤来查找 x 和 y 坐标。
