步骤 1:调查备择树
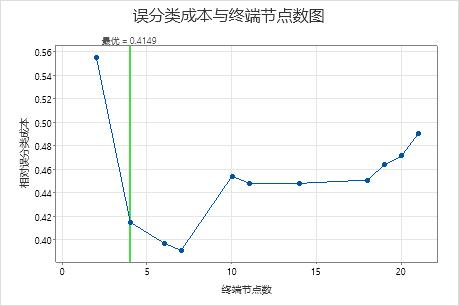
误分类成本与终端节点数的关系图显示了生成最优树的序列中每个树的误分类成本。默认情况下,初始最优树是误分类成本在误分类成本最低树的一个标准误内的最小树。当分析使用交叉验证或检验数据集时,误分类成本来自于验证样本。验证样本的误分类成本通常趋于平稳,并最终随着树变大而增加。
- 最优树是误分类成本降低的模式的一部分。具有更多个节点的一个或多个树属于同一模式。通常,您希望从树进行预测,并尽可能地提高预测准确度。如果树足够简单,您还可以使用它来了解每个预测变量如何影响响应值。
- 最优树是误分类成本相对平直的模式的一部分。与最优树相比,模型汇总统计量相似的一个或多个树的节点要少得多。通常,树的终端节点越少,越能清晰地显示每个预测变量如何影响响应值。较小的树也更易于识别一些目标组,以便进一步研究。如果较小树的预测准确度差异可以忽略不计,则也可以使用较小的树来评估响应变量与预测变量之间的关系。
模型汇总
| 总预测变量 | 13 |
|---|---|
| 重要预测变量 | 13 |
| 终端节点数 | 4 |
| 最小终端节点大小 | 27 |
| 统计量 | 训练 | 测试 |
|---|---|---|
| 负对数似然平均值 | 0.4772 | 0.5164 |
| ROC 曲线下面积 | 0.8192 | 0.8001 |
| 95% 置信区间 | (0.3438, 1) | (0.7482, 0.8520) |
| 提升 | 1.6189 | 1.8849 |
| 误分类成本 | 0.3856 | 0.4149 |
关键结果:具有 4 个节点的树的绘图和模型汇总
序列中具有 4 个节点的树的误分类成本接近 0.41。误分类成本降低时的模式在 4 节点树之后会继续。在这种情况下,分析人员选择探索其他一些误分类成本更低的简单树。
模型汇总
| 总预测变量 | 13 |
|---|---|
| 重要预测变量 | 13 |
| 终端节点数 | 7 |
| 最小终端节点大小 | 5 |
| 统计量 | 训练 | 测试 |
|---|---|---|
| 负对数似然平均值 | 0.3971 | 0.5094 |
| ROC 曲线下面积 | 0.8861 | 0.8200 |
| 95% 置信区间 | (0.5590, 1) | (0.7702, 0.8697) |
| 提升 | 1.9376 | 1.8165 |
| 误分类成本 | 0.2924 | 0.3909 |
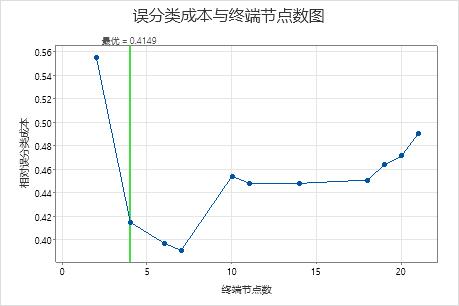
关键结果:具有 7 个节点的树的绘图和模型汇总
将相对交叉验证误分类成本降至最低的分类树有 7 个终端节点,相对误分类成本约为 0.39。如 ROC 曲线下面积等其他统计量也可确认 7 节点树的性能优于 4 节点树。由于 7 节点树的节点不是很多,而且也容易解释,因此分析人员决定使用 7 节点树来研究重要变量并进行预测。
步骤 2:调查树状图上纯度最高的终端节点
选择树后,调查图上纯度最高的终端节点。蓝色表示事件水平,红色表示非事件水平。
注意
可以右键单击树状图来显示树的节点分裂视图。当您有一个大型树并且只想查看分裂节点的变量时,此视图非常有用。
节点继续分裂,直到终端节点无法再为了进一步分组而进行分裂。大多为蓝色的节点表示事件水平占比大。大多为红色的节点表示非事件水平占比大。
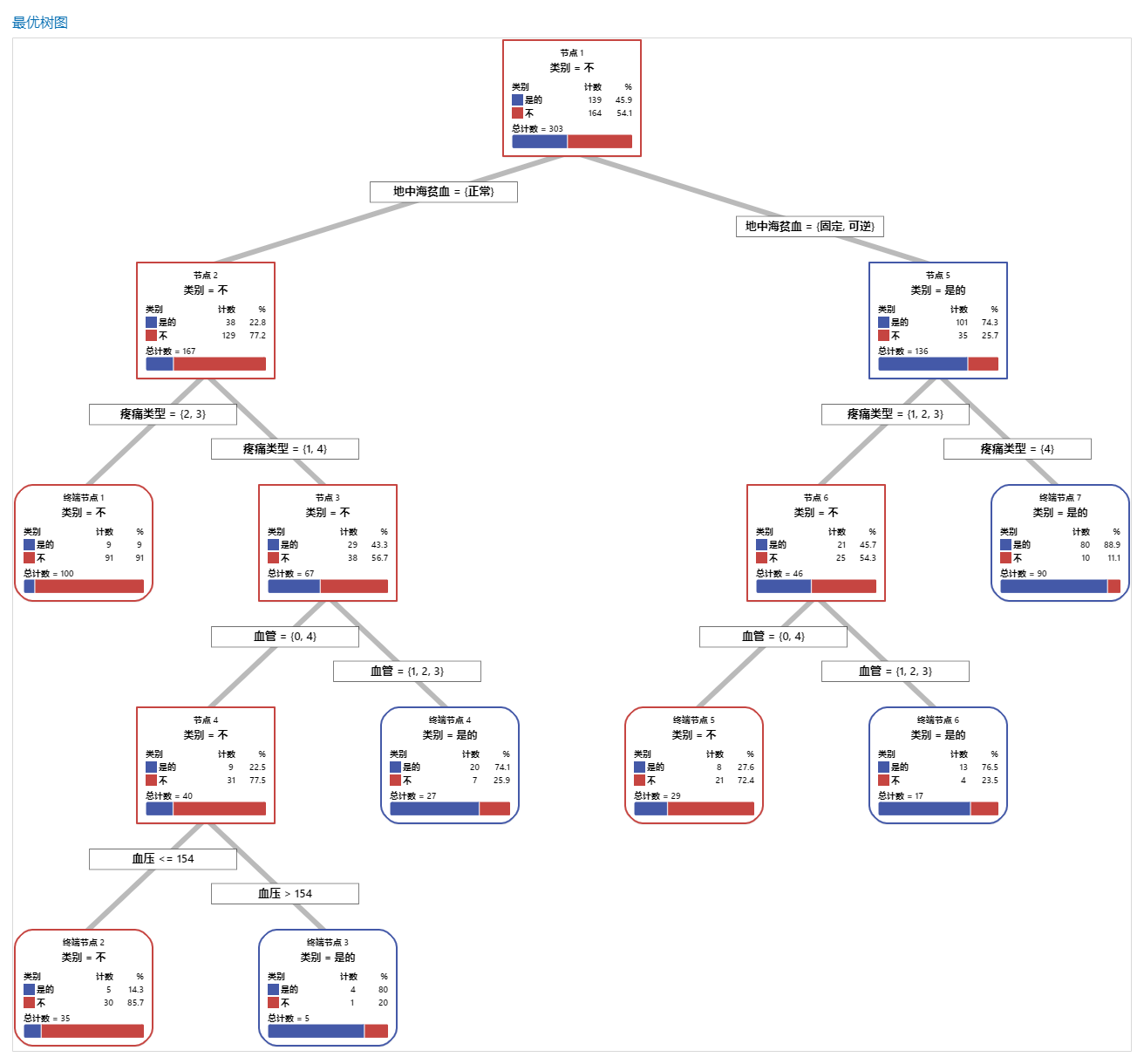
关键结果:树状图
此分类树有 7 个终端节点。蓝色表示事件水平(是),红色表示非事件水平(否)。树状图使用训练数据集。您可以在详细视图和节点分裂视图之间切换树的视图。
- 节点 2:THAL 为“正常”的案例有 167 个。在这 167 个案例中,有 38 个或 22.8% 为“是”,129 个或 77.2% 为“否”。
- 节点 5:THAL 为“固定”或“可逆”的案例有 136 个。在这 136 个案例中,有 101 个或 74.3% 为“是”,35 个或 25.7% 为“否”。
左侧子节点和右侧子节点的下一个分裂变量为“胸痛类型”,疼痛等级为 1、2、3 或 4。节点 2 是终端节点 1 的父节点,节点 5 是终端节点 7 的父节点。
- 终端节点 1:对于 100 个案例,THAL 为“正常”,“胸痛”为 2 或 3。在这 100 个案例中,有 9 个或 9% 为“是”,91 个或 91% 为“否”。
- 终端节点 7:对于 90 个病例,THAL 为“固定”或“可逆”,“胸痛”为 4。在这 90 个案例中,有 80 个或 88.9% 为“是”,10 个或 11.1% 为“否”。
步骤 3:确定重要变量
使用相对变量重要性图来确定哪些预测变量是树最重要的变量。
重要变量是树中的主分裂变量或代理分裂变量。改进得分最高的变量设置为最重要的变量,其他变量依次排序。相对变量重要性将重要性值标准化,以便于解释。相对重要性定义为相对于最重要预测变量的改进百分比。
相对变量重要性的值范围是 0% 到 100%。最重要变量的相对重要性始终为 100%。如果变量不在树中,则该变量就不重要。
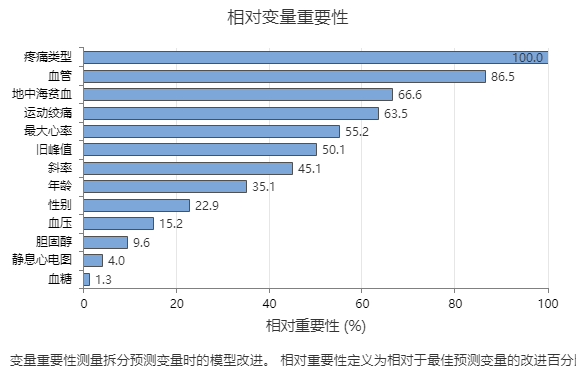
关键结果:相对变量重要性
- 的重要性约为疼痛类型的 87%血管。
- 地中海贫血 的重要性 运动绞痛 都是 疼痛类型的 65% 左右。
- 的重要性约为疼痛类型的 55%最大心率。
- 的重要性约为疼痛类型的 50%旧峰值。
- 斜率、 年龄、 性别 血压 、 和 的重要性远低于 疼痛类型。
尽管它们具有积极的重要性,但分析师可能会认为 胆固醇、 静息心电图和 血糖 不是树的重要贡献者。
步骤 4:评估树的预测能力
最准确的树是误分类成本最低的树。有时,误分类成本稍高的更简单树也比较准确。您可以使用误分类成本与终端节点图来识别替代树。
接受者抽检特征 (ROC) 曲线显示树对数据的分类效果。ROC 曲线在 y 轴上绘制真阳率,在 x 轴上绘制假阳率。真阳率也称为功效。假阳率也称为 I 类错误。
当分类树可以在响应变量中很好地分隔类别时,ROC 曲线下面积为 1,这是可能的最优分类模型。或者,如果分类树无法区分类别并完全随机进行分配,则 ROC 曲线下面积为 0.5。
使用验证技术构建树时,Minitab 会提供树在训练和验证(检验)数据上的性能的相关信息。当曲线很接近时,您可以更确信树没有过度拟合。具有检验数据的树的性能表明了树预测新数据的准确程度。
- 真阳率 (TPR) = 正确预测事件案例的概率
- 假阳率 (FPR) = 非事件案例预测错误的概率
- 假阴率 (FNR) = 事件案例预测错误的概率
- 真阴率 (TNR) = 正确预测非事件案例的概率
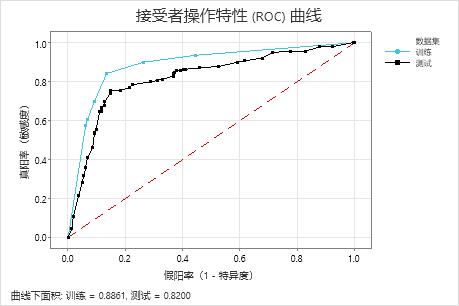
关键结果:接受者抽检特征 (ROC) 曲线
对于此示例,ROC 曲线下面积对于训练为 0.886,对于检验为 0.82。这些值表明分类树在大多数应用中是比较合理的分类器。
混淆矩阵
| 预测类别(训练) | 预测类别(测试) | ||||||
|---|---|---|---|---|---|---|---|
| 实际类别 | 计数 | 是的 | 不 | 正确百分比 | 是的 | 不 | 正确百分比 |
| 是的 (事件) | 139 | 117 | 22 | 84.2 | 105 | 34 | 75.5 |
| 不 | 164 | 22 | 142 | 86.6 | 24 | 140 | 85.4 |
| 全部 | 303 | 139 | 164 | 85.5 | 129 | 174 | 80.9 |
| 统计量 | 训练 (%) | 测试 (%) |
|---|---|---|
| 真阳率(敏感度或功效) | 84.2 | 75.5 |
| 假阳率(I 类错误) | 13.4 | 14.6 |
| 假阴率(II 类错误) | 15.8 | 24.5 |
| 真阴率(特异度) | 86.6 | 85.4 |
关键结果:混淆矩阵
- 真阳率 (TPR) = 训练数据为 84.2%,检验数据为 75.5%
- 假阳率 (FPR) = 训练数据为 13.4%,检验数据为 14.6%
- 假阴性 (FNR) = 训练数据为 15.8%,检验数据为 24.5%
- 真阴性 (TNR) = 训练数据为 86.6%,检验数据为 85.4%
总体而言,训练数据的正确百分比为 85.5%,检验数据的正确百分比为 80.9%。
