后验概率指的是将观测值分配到已给定数据的组的概率。先验概率指的是在您收集数据之前数据已划入某个组的概率。例如,如果正在对特定车辆的买主进行分类,则可能已经知道 60% 的买主为男性,40% 的买主为女性。如果知道或可以估计这些概率,则判别分析可以使用这些先验概率来计算后验概率。未指定先验概率时,Minitab 假定这些组有同等概率。
假定数据呈正态分布,线性判别函数按 ln(pi) 增加,其中 pi 是组 i 的先验概率。由于观测值按最小的广义距离(或者对等的最大线性判别函数)分配到组,则会产生这样的影响:具有高先验概率的组后验概率增加。
注意
如果指定先验概率,则可以显著影响结果的准确性。调查组间的不相等比率是否表明实际总体中的真正差异,或者是否由于取样误差而导致该差异。
现在,假定我们有先验概率,并且假定 fi(x) 是组 i 中数据的联合密度(用样本估计值替换了总体参数)。
后验概率是给定数据并按以下方式计算的组 i 的概率:
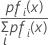
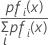
最大后验概率等于 ln [pifi(x)] 的最大值。
如果 fi(x) 是正态分布,则:
ln [pifi(x)] = -.-.-.-.5 [di2(x) – 2 ln pi] –(常量)
方括号中的项称为 x 到组 i 的广义平方距离,由 di2(x) 表示。注意,
di2(x) = -2[mi' Sp-1 x - ..5 mi' Sp-1mi + ln pi] + x' Sp-1x
方括号中的项是线性判别函数。与没有先验概率的案例的唯一区别是常量项发生了变化。请注意,最大后验概率等于最小广义距离,该距离等于最大线性判别函数。
