简单对应分析的行贡献和列贡献

列剖面处于 d 维空间中。完整的 d 主轴集张成此空间。假定 g_j1, g_j2, g_j3, ..., g_jd 是主轴列剖面 j 的坐标。这些坐标称为列主坐标。列剖面 j 的第 k 个主坐标是 g_jk。

最佳 k 维子空间由前 k 个主轴张成。如果将列剖面 j 投影到最佳 k 维子空间，g_j1, ..., g_jk 是此子空间中剖面的列主坐标。

每个主轴对每行的惯量提供贡献。行 i 和分量 k 的相关是主轴 k 对行 i 惯量的贡献，表示为行 i 惯量的百分比。

相关还可以视为行剖面 i 和主分量 k 之间的相关。该相关计算如下：

同样地，列 j 和分量 k 的相关是主轴 k 对列 j 的贡献，表示为列 j 的惯量百分比。

相关还可视为列剖面 j 和主分量 k 之间的相关。该相关计算如下：

Minitab 显示给定行或列的相对惯量。绝对惯量等于相对惯量和总惯量的乘积。

所有主分量的行 i（列 j）的相关之和为 1。前 k 个主坐标之和是与行剖面 i（列剖面 j）相关的质量和最佳 k 维子空间。

表示法

单元格中的惯量计算如下：

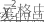
所有单元格惯量的总和是表的总惯量，有时简称为惯量。

单元格的相对惯量计算如下：

列剖面处于 c 维空间中。低维子空间由主轴（亦称为主分量）张成。选择第一个主轴作为 c 维空间中的向量，其在总惯量中占最大比例。因此，第一个主轴张成最佳（即，最靠近使用相应度量的剖面）单维子空间。选择第二个主轴作为 c 维空间中的向量，其在剩余惯量中占最大比例。因此，前两个主轴张成最佳二维子空间。选择第三个主轴作为 c 维空间中的向量，其在前两个主轴所占惯量后的剩余惯量中占最大比例。因此，前三个主轴张成最佳三维子空间，以此类推。

假设 d = (r − 1) 和 (c − 1) 中的较小者。行剖面（或对等的列剖面）实际位于全 c 维空间（或对等的全 r 维空间）中。因此，主轴数最大为 d。

与行剖面 i 和最佳 k 维子空间相关的质量计算如下：

与列剖面 j 和最佳 k 维子空间相关的质量计算如下：

质量始终是一个介于 0 和 1 之间的数字，数字越大，表示近似程度越高。

表示法

每行对每个轴惯量提供贡献。行 i 对轴 k 的贡献表示为轴 k 的惯量百分比，计算如下：

主轴 k 的贡献之和（在所有行 i 上）为 1。

同样地，每列对每个轴惯量提供贡献。列 j 对 k 的贡献表示为轴 k 的惯量百分比，计算如下：

主轴 k 的贡献之和（在所有列 j 上）为 1。

表示法

行 i 的总量计算如下：

列 j 的总量计算如下：

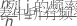
r 行总量的向量与平均行剖面相同，c 列总量的向量与平均列剖面相同。