行图
注意
默认情况下,Minitab 显示前两个主分量的点,这两个主分量占总惯量的最大比例。要在图上显示其他主分量(轴),请单击图形并在执行分析时输入分量数。
解释
使用行图可找出行类别之间的关系,并帮助解释与行类别相关的主分量。距原点很远的点表明类别具有更大影响力。在图两端的点表明分量对这些类别进行对照
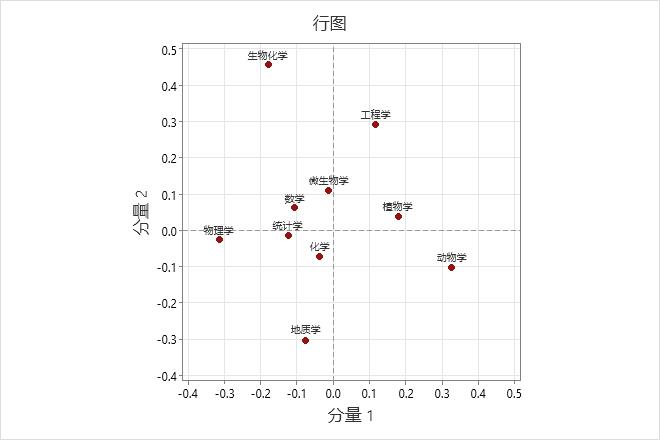
此行图显示行主坐标。分量 1(最好地解释了“动物学”和“物理学”)显示这两个领域距原点最远,但使用的符号相反。因此,分量 1 使生物科学“动物学”和“植物学”与“物理学”形成对照。分量 2 使“生物化学”和“工程学”与“地质学”形成对照。
列图
注意
默认情况下,Minitab 显示前两个主分量的点,这两个主分量占最大比率的总惯量。要在图上显示其他主分量(轴),请单击图形并在执行分析时输入分量数。
解释
使用列图可找出列类别之间的关系,并帮助解释与列类别相关的主分量。距原点更远的点表明类别具有更大的影响力。在图两端的点表明分量使这些类别形成对照。
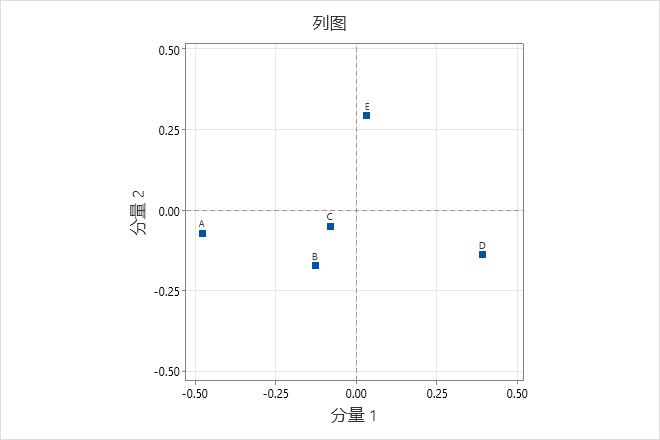
此列图显示列主坐标。分量 1(最好地解释了经费类别 A 和 D)显示这两个类别距原点最远,但使用的符号相反。因此,分量 1 使这两个经费类别形成对照。分量 2 最好地解释了经费类别 E,并且使此类别与其他经费类别形成对照。
对称图
注意
默认情况下,Minitab 显示前两个主分量的点,这两个主分量占最大比率的总惯量。要在图上显示其他主分量(轴),请单击图形并在执行分析时输入分量数。
解释
重要信息
对称图中行到列的距离使用两种不同的映射。由于行到列的距离并未标准化,行类别和列类别之间的距离不容易解释。要解释行类别和列类别之间的距离,请使用非对称图。
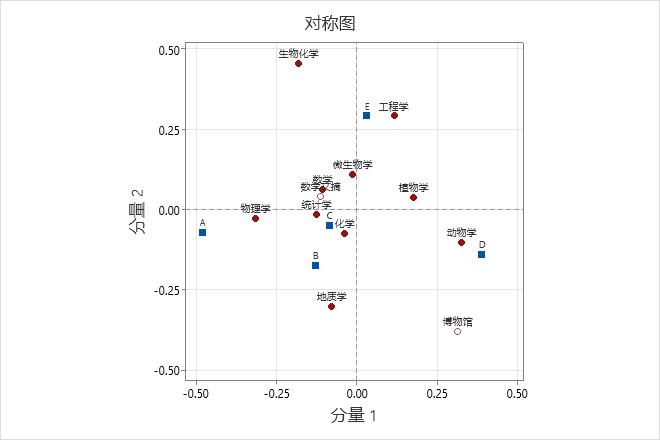
此对称图显示行列主坐标图。分量 1(最好地解释了“动物学”和“物理学”)显示这两个领域距原点最远,但使用的符号相反。分量 1 使列类别 A 与列类别 D 形成对照。分量 2 使行类别“生物化学”和“工程学”与“地质学”和“博物馆研究”形成对照,并且最好地解释了列类别 E。
非对称行图
注意
默认情况下,Minitab 显示前两个主分量的点,这两个主分量占最大比率的总惯量。要在图上显示其他主分量(轴),请单击图形并在执行分析时输入分量数。
解释
使用非对称行图可找出行类别和列类别之间的关系,并帮助解释主分量。距原点更远的点表明类别具有更大的影响力。在图两端的点表明分量使这些类别形成对照。行类别的点距列类别的点越近,列类别的行剖面的值越高。
注意
非对称图可让您直观地解释行点与列点之间的距离,尤其是在两个分量在总惯量中占较大比率时。但是,非对称图中的点在图形中心位置可能会彼此靠的特别近,这样便很难查看结果。在这种情况下,您可能还要显示对称图,从而更为清楚地查看行类别或列类别之间的关系。
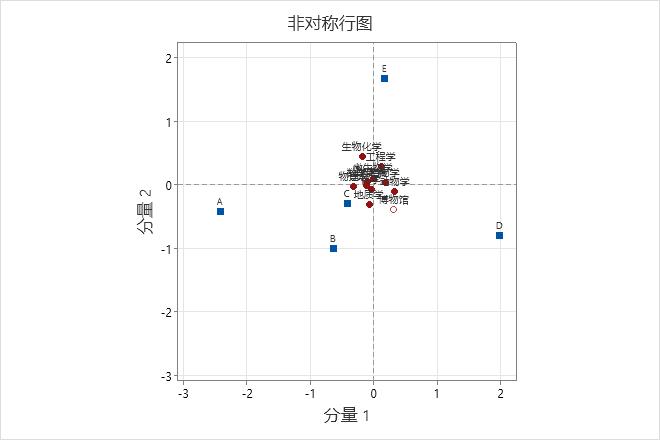
在此非对称行图中,行点代表学术科目,列点代表经费水平(A 是最高经费水平,D 是最低经费水平,E 说明没有经费)。
在经费类中,分量 1 使各个经费水平形成对照,而分量 2 使已提供经费类(A 到 D)与未提供经费类 (E) 形成对照。在各学科中,“物理学”的经费水平往往最高,而“动物学”的经费水平最低。“生物化学”往往没有提供经费,但提供经费时,很少在最低经费列表 (D) 中。在这些学术领域中,“生物化学”距列类别 E 最近,这表示生物化学作为一门学科,其未获得经费的研究人员在此项研究中所占的百分比最高。“博物馆研究”通常都获得经费,但水平比学术研究人员低。但是,图形中心的点聚类使得结果很难查看。为了更轻松地解释与学术科目相关的分量,还要检查非对称列图或对称行图。
非对称列图
注意
默认情况下,Minitab 显示前两个主分量的点,这两个主分量占最大比率的总惯量。要在图上显示其他主分量(轴),请单击图形并在执行分析时输入分量数。
解释
使用非对称行图可找出行类别和列类别之间的关系,并帮助解释主分量。距原点更远的点表明类别具有更大的影响力。在图两端的点表明分量使这些类别形成对照。行类别的点距列类别的点越近,列类别的列剖面的值越高。
注意
非对称图可让您直观地解释行点与列点之间的距离,尤其是在两个分量在总惯量中占较大比率时。但是,非对称图中的点在图形中心位置可能会彼此靠的特别近,这样便很难查看结果。在这种情况下,您可能还要显示对称图,从而更为清楚地查看行类别或列类别之间的关系。
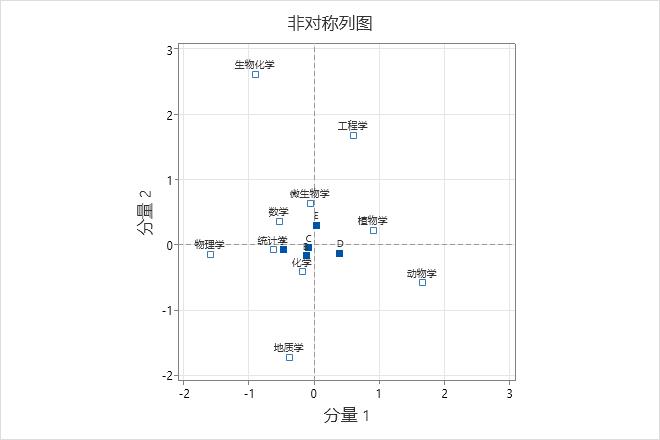
在此非对称列图中,行点代表学术科目,列点代表经费水平(A 是最高经费水平,D 是最低经费水平,E 说明没有经费)。
在学科中,分量 1 使“物理学”与“动物学”形成对照,而分量 2 使“生物化学”与“地质学”形成对照。在经费类中,分量 1 使各个经费水平形成对照,而分量 2 使已提供经费类(A 到 D)与未提供经费类 (E) 形成对照。“物理学”的经费水平往往最高,而“动物学”的经费水平最低。越靠近图中心的系往往具有类似于总体经费剖面的经费剖面。经费类别 E 最靠近行类别“微生物学”,这说明类别 E 的微生物学研究人员百分比最高。
