特征值
特征值(亦称为特征根)表示主分量的方差。
解释
可使用特征值的大小确定主分量数。保留具有最大特征值的主分量。例如,使用 Kaiser 标准时,只能使用特征值大于 1 的主分量。
为了直观地比较特征值的大小,请使用碎石图。碎石图可帮助您基于特征值的大小确定分量数。
相关矩阵的特征分析
| 特征值 | 3.5476 | 2.1320 | 1.0447 | 0.5315 | 0.4112 | 0.1665 | 0.1254 | 0.0411 |
|---|---|---|---|---|---|---|---|---|
| 比率 | 0.443 | 0.266 | 0.131 | 0.066 | 0.051 | 0.021 | 0.016 | 0.005 |
| 累积 | 0.443 | 0.710 | 0.841 | 0.907 | 0.958 | 0.979 | 0.995 | 1.000 |
特征向量
| 变量 | PC1 | PC2 | PC3 | PC4 | PC5 | PC6 | PC7 | PC8 |
|---|---|---|---|---|---|---|---|---|
| 收入 | 0.314 | 0.145 | -0.676 | -0.347 | -0.241 | 0.494 | 0.018 | -0.030 |
| 教育程度 | 0.237 | 0.444 | -0.401 | 0.240 | 0.622 | -0.357 | 0.103 | 0.057 |
| 年龄 | 0.484 | -0.135 | -0.004 | -0.212 | -0.175 | -0.487 | -0.657 | -0.052 |
| 住址 | 0.466 | -0.277 | 0.091 | 0.116 | -0.035 | -0.085 | 0.487 | -0.662 |
| 服务处所 | 0.459 | -0.304 | 0.122 | -0.017 | -0.014 | -0.023 | 0.368 | 0.739 |
| 储蓄 | 0.404 | 0.219 | 0.366 | 0.436 | 0.143 | 0.568 | -0.348 | -0.017 |
| 外债 | -0.067 | -0.585 | -0.078 | -0.281 | 0.681 | 0.245 | -0.196 | -0.075 |
| 信用卡数量 | -0.123 | -0.452 | -0.468 | 0.703 | -0.195 | -0.022 | -0.158 | 0.058 |
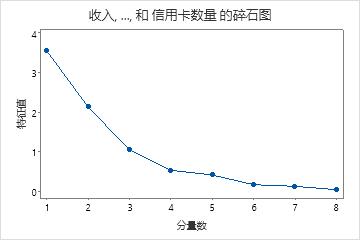
在这些结果中,前三个主分量的特征值大于 1。这三个分量解释 84.1% 的数据变异。此碎石图显示特征值在第三个主分量之后开始形成直线。
比率
比率指的是每个主分量解释的数据变异性比率。
解释
可以使用该比率确定哪些主分量解释大部分数据变异性。比率越高表明主分量解释的变异性越多。比率的大小可帮助您确定主分量是否足够重要,需要保留。
例如,比率为 0.621 的主分量解释 62.1% 的数据变异性。因此,此分量很重要,应包括在其中。另外一个分量的比率为 0.005,因此只解释 0.5% 的变异性。此分量可能不够重要,无需包括在其中。
累积
累积是由连续主分量解释的样本变异性的累积比率。
解释
使用累积比率可评估连续主分量解释的总方差量。累积比率可帮助您确定要使用的主分量数。保留解释可接受方差水平的主分量。可接受水平取决于您的应用。
例如,您可能只需要主分量解释的 80% 的方差。但如果您要对这些数据执行其他分析,则可能需要主分量至少解释 90% 的方差。
主分量 (PC)
注意
如果使用相关矩阵,则必须对这些变量进行标准化,以便获得正确的分量分值。
解释
要解释每个主分量,请检查原始变量系数的量值和方向。系数的绝对值越大,对应变量在计算分量时就越重要。系数的绝对值多大才视为重要具有主观性。请运用您的专业知识确定相关值在哪个水平才算重要。
相关矩阵的特征分析
| 特征值 | 3.5476 | 2.1320 | 1.0447 | 0.5315 | 0.4112 | 0.1665 | 0.1254 | 0.0411 |
|---|---|---|---|---|---|---|---|---|
| 比率 | 0.443 | 0.266 | 0.131 | 0.066 | 0.051 | 0.021 | 0.016 | 0.005 |
| 累积 | 0.443 | 0.710 | 0.841 | 0.907 | 0.958 | 0.979 | 0.995 | 1.000 |
特征向量
| 变量 | PC1 | PC2 | PC3 | PC4 | PC5 | PC6 | PC7 | PC8 |
|---|---|---|---|---|---|---|---|---|
| 收入 | 0.314 | 0.145 | -0.676 | -0.347 | -0.241 | 0.494 | 0.018 | -0.030 |
| 教育程度 | 0.237 | 0.444 | -0.401 | 0.240 | 0.622 | -0.357 | 0.103 | 0.057 |
| 年龄 | 0.484 | -0.135 | -0.004 | -0.212 | -0.175 | -0.487 | -0.657 | -0.052 |
| 住址 | 0.466 | -0.277 | 0.091 | 0.116 | -0.035 | -0.085 | 0.487 | -0.662 |
| 服务处所 | 0.459 | -0.304 | 0.122 | -0.017 | -0.014 | -0.023 | 0.368 | 0.739 |
| 储蓄 | 0.404 | 0.219 | 0.366 | 0.436 | 0.143 | 0.568 | -0.348 | -0.017 |
| 外债 | -0.067 | -0.585 | -0.078 | -0.281 | 0.681 | 0.245 | -0.196 | -0.075 |
| 信用卡数量 | -0.123 | -0.452 | -0.468 | 0.703 | -0.195 | -0.022 | -0.158 | 0.058 |
在这些结果中,第一个主分量与年龄、居住年限、服务处所和存款具有较大的正关联,因此,您可以将此分量解释为主要度量申请者的长期财务稳定性。第二个分量与外债和信用卡数具有较大的负关联,因此,此分量主要度量申请者的信用历史。第三个分量与收入、教育程度和信用卡数具有较大的负关联,因此,此分量主要度量申请者的学术和收入证明。
分值
分值是每个主分量的系数确定的数据的线性组合。要获取观测值的分值,请替换主分量线性方程中的值。如果使用相关矩阵,则必须对这些变量进行标准化,以便在使用线性方程时获得正确分量分值。
注意
要获取每个观测值的计算分值,请单击存储并在执行分析时输入要在工作表中存储分值的列。要在图形中直观地显示第一个和第二个分量的分值,请单击图形并在执行分析时选择分值图。
相关矩阵的特征分析
| 特征值 | 3.5476 | 2.1320 | 1.0447 | 0.5315 | 0.4112 | 0.1665 | 0.1254 | 0.0411 |
|---|---|---|---|---|---|---|---|---|
| 比率 | 0.443 | 0.266 | 0.131 | 0.066 | 0.051 | 0.021 | 0.016 | 0.005 |
| 累积 | 0.443 | 0.710 | 0.841 | 0.907 | 0.958 | 0.979 | 0.995 | 1.000 |
特征向量
| 变量 | PC1 | PC2 | PC3 | PC4 | PC5 | PC6 | PC7 | PC8 |
|---|---|---|---|---|---|---|---|---|
| 收入 | 0.314 | 0.145 | -0.676 | -0.347 | -0.241 | 0.494 | 0.018 | -0.030 |
| 教育程度 | 0.237 | 0.444 | -0.401 | 0.240 | 0.622 | -0.357 | 0.103 | 0.057 |
| 年龄 | 0.484 | -0.135 | -0.004 | -0.212 | -0.175 | -0.487 | -0.657 | -0.052 |
| 住址 | 0.466 | -0.277 | 0.091 | 0.116 | -0.035 | -0.085 | 0.487 | -0.662 |
| 服务处所 | 0.459 | -0.304 | 0.122 | -0.017 | -0.014 | -0.023 | 0.368 | 0.739 |
| 储蓄 | 0.404 | 0.219 | 0.366 | 0.436 | 0.143 | 0.568 | -0.348 | -0.017 |
| 外债 | -0.067 | -0.585 | -0.078 | -0.281 | 0.681 | 0.245 | -0.196 | -0.075 |
| 信用卡数量 | -0.123 | -0.452 | -0.468 | 0.703 | -0.195 | -0.022 | -0.158 | 0.058 |
在这些结果中,可使用 PC1 下列出的系数根据标准化数据计算第一个主分量的分值。
PC1 = 0.314 收入 + 0.237 教育程度 + 0.484 年龄 + 0.466 居住年限 + 0.459 服务处所 + 0.404 储蓄 - 0.067 外债 - 0.123 信用卡数
距离
Mahalanobis 距离是数据点与多变量空间的质心(总体均值)之间的距离。
注意
要计算每个观测值的距离,请单击存储,并在您执行分析时输入要在工作表中存储距离的列。要在图形中显示距离,请单击图形并在执行分析时选择异常值图。
解释
使用 Mahalanobis 距离标识异常值。与每次检验一个变量来检测异常值相比,检查 Mahalanobis 距离是一种功能更强大的多变量方法,因为它会考虑变量之间的不同尺度以及变量间的相关程度。
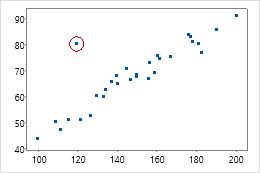
例如,单独考虑时,带圆圈的数据点的 x 值或 y 值均无异常。但是,数据点与两个变量的相关结构不拟合。因此,这个点的 Mahalanobis 距离异常大。
要评估距离值是否足够大以将观测值视为异常值,请使用异常值图。
碎石图
碎石图显示主分量数与对应的特征值。碎石图按从最大到最小的顺序排列特征值。相关矩阵的特征值等于主分量的方差。
要显示碎石图,请在执行分析时单击图形并选择碎石图。
解释

此碎石图显示特征值在第三个主分量之后开始形成直线。因此,剩余的主分量在变异性中所占比率非常小(接近于零),并且可能不重要。
分值图
分值图相对于第一个主分量分值绘制出第二个主分量分值。
要显示分值图,请在执行分析时单击图形并选择分值图。
解释
如果前两个分量在数据变异中占大部分比率,则可以使用分值图评估数据结构并检测聚类、异常值和趋势。该图的数据分组情况可以说明数据中两种或两种以上不同的分布。如果数据遵循正态分布,并且不存在异常值,则这些点将随机分布在零的周围。
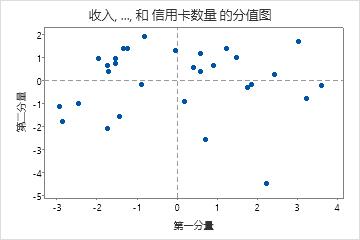
在此分值图中,位于右下角的点可能是异常值。您应调查此点。
提示
要查看每个观测值的计算分值,请将指针放在图形中数据点之上。要为其他分量创建分值图,请存储分值并使用。
载荷图
载荷图相对于第二个分量的系数绘制出第一个分量各变量的系数。系数是构成每个主成分的特征向量的值。这些系数表明分量中每个变量的相对权重。
要显示载荷图,请在执行分析时单击图形并选择载荷图。
解释
使用载荷图可标识哪些变量对每个分量的影响最强。系数的范围可以从 -1 到 1。接近 -1 或 1 的系数表示变量对分量有很强的影响。接近 0 的系数表示变量对分量的影响较弱。评估系数还可以帮助您根据变量表征每个分量。
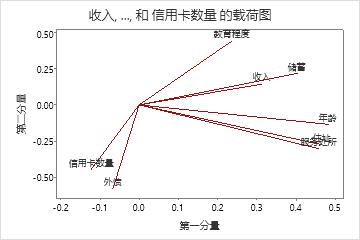
在此载荷图中,年龄、居住年限、服务处所和存款在分量 1 上具有较大的正载荷。因此,此分量主要度量申请者的财务稳定性。债务和信用卡在组件 2 上具有较大的负系数,因此该组件主要衡量申请人的信用记录。
双标图
双标图与分值图和载荷图重叠。
要显示双标图,请单击图形,并在执行分析时选择双标图。
解释
使用双标图可在一个图形中评估前两个分量的数据结构和载荷。Minitab 相对于第一个主分量分值绘制第二个主分量分值以及这两个分量的载荷。
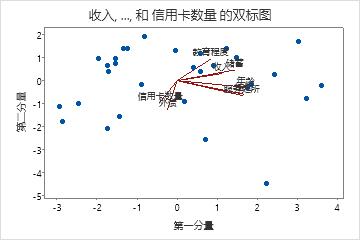
- 年龄、居住年限、服务处所和存款在分量 1 上具有较大的正载荷。因此,此分量侧重于申请者的长期财务稳定性。
- 外债和信用卡数量在分量 2 上具有较大的负载荷。因此,此分量侧重于申请者的信用历史。
- 位于右下角的点可能是异常值。您应调查此点。
异常值图
异常值图显示各个观测值的 Mahalanobis 距离和标识异常值的参考线。Mahalanobis 距离是各数据点与多变量空间的质心(总体均值)之间的距离。与每次检验一个变量来检测异常值相比,检查 Mahalanobis 距离是一种功能更强大的方法,因为它会考虑变量之间的不同尺度以及变量间的相关程度。
要显示异常值图,您必须单击图形并在执行分析时选择异常值图。
解释
使用异常值图可标识异常值。参考线之上的任何点都是异常值。
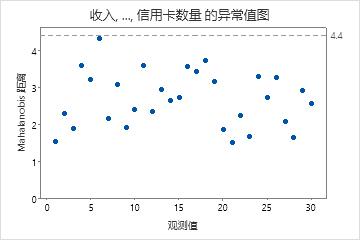
在这些结果中,没有异常值。所有点都在参考线之下。
提示
将指针放在异常值图中任何点之上以确认观测值。使用 可刷出该异常值图中的多个异常值,并在工作表中标记观测值。
