步骤 1:确定主分量数
使用惯量比率可确定占大部分数据预期值偏差的最小主分量(亦称为主轴)数量。保留解释可接受总惯量比率的主分量。可接受水平取决于您的应用。理想情况下,第一个、前两个或前三个分量占总惯量的大部分比率。
如果需要的最小主分量数量与您为分析输入的分量数不匹配,请使用相应数量的分量重新执行分析。
指示符矩阵分析
| 轴 | 惯量 | 比率 | 累积 | 直方图 |
|---|---|---|---|---|
| 1 | 0.4032 | 0.4032 | 0.4032 | ****************************** |
| 2 | 0.2520 | 0.2520 | 0.6552 | ****************** |
| 3 | 0.1899 | 0.1899 | 0.8451 | ************** |
| 4 | 0.1549 | 0.1549 | 1.0000 | *********** |
| 合计 | 1.0000 |
主要结果:轴、比率、累积比率
这些结果显示将总惯量分解成 4 个分量。这 4 个分量解释的总惯量是 1.000。在总惯量中,第一个分量(轴)占惯量的 40.32%,第二个分量占惯量的 25.20%。这两个变量总共占总惯量的 65.52%。因此,为分析指定 2 个分量可能不够。添加第 3 个分量可将惯量的累积比率增加到 84.51%。
步骤 2:解释主分量
使用质量值可以为每个类别确定分量所占的惯量比率。“质量”始终是介于 0 和 1 之间的数字。质量值越大,分量对类别的表示越好。值越小,对类别的表示越差。质量值帮助解释分量。
使用列的贡献值可评估对每个分量的惯量贡献最大的类别。为了直观地解释分量,请使用列图。
指示符矩阵分析
| 轴 | 惯量 | 比率 | 累积 | 直方图 |
|---|---|---|---|---|
| 1 | 0.4032 | 0.4032 | 0.4032 | ****************************** |
| 2 | 0.2520 | 0.2520 | 0.6552 | ****************** |
| 3 | 0.1899 | 0.1899 | 0.8451 | ************** |
| 4 | 0.1549 | 0.1549 | 1.0000 | *********** |
| 合计 | 1.0000 |
列贡献
| 分量 1 | 分量 2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ID | 名称 | 二次 | 质量 | 惯性 | 坐标 | 相关 | 贡献 | 坐标 | 相关 | 贡献 |
| 1 | 小型 | 0.9655 | 0.0424 | 0.2076 | 0.3814 | 0.0297 | 0.0153 | -2.1394 | 0.9357 | 0.7707 |
| 2 | 标准 | 0.9655 | 0.2076 | 0.0424 | -0.0780 | 0.0297 | 0.0031 | 0.4374 | 0.9357 | 0.1576 |
| 3 | 未弹出 | 0.4739 | 0.2134 | 0.0366 | -0.2844 | 0.4717 | 0.0428 | -0.0197 | 0.0023 | 0.0003 |
| 4 | 弹出 | 0.4739 | 0.0366 | 0.2134 | 1.6587 | 0.4717 | 0.2497 | 0.1151 | 0.0023 | 0.0019 |
| 5 | Collis | 0.6133 | 0.1926 | 0.0574 | -0.4264 | 0.6095 | 0.0868 | 0.0338 | 0.0038 | 0.0009 |
| 6 | 翻车 | 0.6133 | 0.0574 | 0.1926 | 1.4294 | 0.6095 | 0.2911 | -0.1133 | 0.0038 | 0.0029 |
| 7 | 不严重 | 0.5680 | 0.1353 | 0.1147 | -0.6523 | 0.5018 | 0.1428 | -0.2371 | 0.0663 | 0.0302 |
| 8 | 严重 | 0.5680 | 0.1147 | 0.1353 | 0.7692 | 0.5018 | 0.1684 | 0.2795 | 0.0663 | 0.0356 |
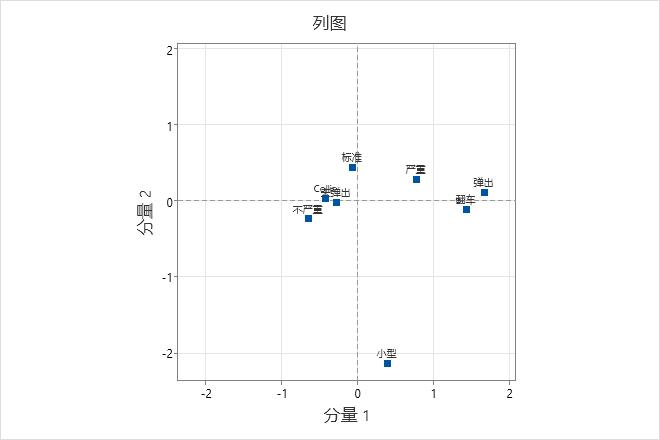
主要结果:质量、贡献、列图
在此项分析中,Minitab 会为与汽车事故相关的数据计算两个主分量。在“列贡献”表中,汽车大小“小型”(0.965) 和“标准”(0.965) 的质量值最高。因此,这两个分量对这两个类别的表示最好。事故严重性的表示最差,其“严重”和“不严重”的质量值均为 0.568。“翻转”(0.291) 和 “弹出”(0.250) 对分量 1 的惯量贡献最大。汽车大小“小型”(0.771) 和“标准”(0.158) 对分量 2 的惯量贡献最大。但是,由于两个变量可能不足以解释这些数据的变异性,因此应谨慎解释这些结果。
列图显示列主坐标。分量 1 通过水平轴上距原点最远的这两个类别最好地解释了“翻车”和“弹出”。“严重”和“不严重”在水平轴上原点的两端。因此,分量 1 使这些类别值形成了对照。分量 2 显示在垂直轴上。分量 2 最好地解释了“小型”汽车大小,并且使其与其他类别形成对照。
步骤 3:检查类别的惯量
检查列类别的计算惯量值。与预期值偏差越大的类别,惯量值越高,对总卡方值的贡献越大。
列贡献
| 分量 1 | 分量 2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ID | 名称 | 二次 | 质量 | 惯性 | 坐标 | 相关 | 贡献 | 坐标 | 相关 | 贡献 |
| 1 | 小型 | 0.9655 | 0.0424 | 0.2076 | 0.3814 | 0.0297 | 0.0153 | -2.1394 | 0.9357 | 0.7707 |
| 2 | 标准 | 0.9655 | 0.2076 | 0.0424 | -0.0780 | 0.0297 | 0.0031 | 0.4374 | 0.9357 | 0.1576 |
| 3 | 未弹出 | 0.4739 | 0.2134 | 0.0366 | -0.2844 | 0.4717 | 0.0428 | -0.0197 | 0.0023 | 0.0003 |
| 4 | 弹出 | 0.4739 | 0.0366 | 0.2134 | 1.6587 | 0.4717 | 0.2497 | 0.1151 | 0.0023 | 0.0019 |
| 5 | Collis | 0.6133 | 0.1926 | 0.0574 | -0.4264 | 0.6095 | 0.0868 | 0.0338 | 0.0038 | 0.0009 |
| 6 | 翻车 | 0.6133 | 0.0574 | 0.1926 | 1.4294 | 0.6095 | 0.2911 | -0.1133 | 0.0038 | 0.0029 |
| 7 | 不严重 | 0.5680 | 0.1353 | 0.1147 | -0.6523 | 0.5018 | 0.1428 | -0.2371 | 0.0663 | 0.0302 |
| 8 | 严重 | 0.5680 | 0.1147 | 0.1353 | 0.7692 | 0.5018 | 0.1684 | 0.2795 | 0.0663 | 0.0356 |
主要结果:列惯量
在“列贡献”表中,标记为“惯量”的列是每个类别贡献的总惯量的比率。因此,“弹出”与其预期值偏差最大,并且贡献总卡方统计量的 21.3%。
