研究人员想要研究不同类别的汽车事故如何彼此相关。根据类型、严重性、汽车大小和司机弹出对汽车事故进行分类。
研究人员使用多重对应分析来检查四因子表中的类别如何彼此相关。
- 打开样本数据集 汽车事故.MWX。
- 选择。
- 选择类别变量并输入汽车重量驾驶者弹出事故类型事故严重性。
- 在类别名称中,输入事故名称。
- 在分量数中,输入 2。
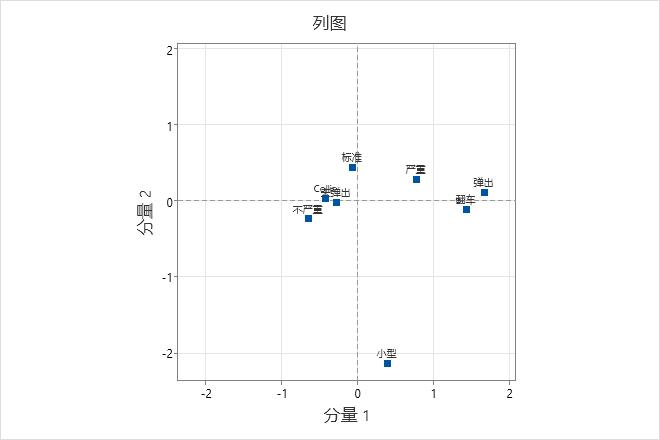
- 单击图形并选择显示列图。
- 单击每个对话框中的确定。
解释结果
“指示符矩阵分析”汇总变量的分解并显示每个分量所占的惯量。在总惯量 1 中,分量(轴)1 约占 40.3%,分量(轴)2 占 25.2%,分量(轴)3 占 19%,分量(轴)4 占 15.5%。累积起来,前 3 个分量占总惯量的 84.5%。
通过使用“列贡献”表和列图,研究人员可以解释与类别相关的分量。在该表中,质量值 (Qual) 表示计算分量所占的列惯量比率。在此示例中,这两个分量对汽车大小类别“小型”和“标准”的表示最佳 (Qual = 0.965)。这两个分量对弹出类别的表示最差 (Qual = 0.474)。标记为“总量”的列是整个数据集中类的比率。“弹出”(0.037) 和“翻转”(0.057) 比较少见。
“坐标”列提供列坐标,这些列坐标显示在列图中。“相关性”(Corr) 代表各个分量对每个类别惯量的贡献。例如,分量 1 占事故类型类别(“碰撞”和“翻转”)惯量的 61%。分量 2 占汽车大小类别“小型”和“标准”惯量的 93.6%。
Contr,即行对轴惯量的贡献,显示“弹出”(Contr = 0.250) 和“翻转”(Contr = 0.291) 对分量 1 贡献最大。汽车大小“小型”(0.771) 和“标准”(0.158) 对分量 2 贡献最大。
在此列图中,“弹出”和“翻转”与沿着分量 1 的水平轴分布的原点最远。这符合对分量 1 的这些类别的贡献 (Contr) 相对较高这一情况。由于“弹出”和“未弹出”以及“严重”和“不严重”处于原点两端,因此分量 1 使这些类别值形成对照。分量 2 显示在垂直轴上。“小型”汽车大小位于垂直轴一端上远离其他类别的位置。因此,分量 2 使“小型”汽车大小与其他类别形成对照。
但是,由于两个变量可能不足以解释这些数据的变异性,因此应谨慎解释这些结果。
指示符矩阵分析
| 轴 | 惯量 | 比率 | 累积 | 直方图 |
|---|---|---|---|---|
| 1 | 0.4032 | 0.4032 | 0.4032 | ****************************** |
| 2 | 0.2520 | 0.2520 | 0.6552 | ****************** |
| 3 | 0.1899 | 0.1899 | 0.8451 | ************** |
| 4 | 0.1549 | 0.1549 | 1.0000 | *********** |
| 合计 | 1.0000 |
列贡献
| 分量 1 | 分量 2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ID | 名称 | 二次 | 质量 | 惯性 | 坐标 | 相关 | 贡献 | 坐标 | 相关 | 贡献 |
| 1 | 小型 | 0.9655 | 0.0424 | 0.2076 | 0.3814 | 0.0297 | 0.0153 | -2.1394 | 0.9357 | 0.7707 |
| 2 | 标准 | 0.9655 | 0.2076 | 0.0424 | -0.0780 | 0.0297 | 0.0031 | 0.4374 | 0.9357 | 0.1576 |
| 3 | 未弹出 | 0.4739 | 0.2134 | 0.0366 | -0.2844 | 0.4717 | 0.0428 | -0.0197 | 0.0023 | 0.0003 |
| 4 | 弹出 | 0.4739 | 0.0366 | 0.2134 | 1.6587 | 0.4717 | 0.2497 | 0.1151 | 0.0023 | 0.0019 |
| 5 | Collis | 0.6133 | 0.1926 | 0.0574 | -0.4264 | 0.6095 | 0.0868 | 0.0338 | 0.0038 | 0.0009 |
| 6 | 翻车 | 0.6133 | 0.0574 | 0.1926 | 1.4294 | 0.6095 | 0.2911 | -0.1133 | 0.0038 | 0.0029 |
| 7 | 不严重 | 0.5680 | 0.1353 | 0.1147 | -0.6523 | 0.5018 | 0.1428 | -0.2371 | 0.0663 | 0.0302 |
| 8 | 严重 | 0.5680 | 0.1147 | 0.1353 | 0.7692 | 0.5018 | 0.1684 | 0.2795 | 0.0663 | 0.0356 |