主成份
在主分量提取方法中,第 j个载荷是第 j个主分量的尺度系数。这些因子与前 m 个分量相关。在非旋转解中,您可以像在主分量分析中解释分量那样解释因子。但是,旋转后,便不能以类似于主分量的方式解释因子。
样本相关矩阵 R(或协方差矩阵 S)的主分量因子分析根据特征值-特征向量对 (λi, ei), i = 1, ..., p 和 λ1 ≤ λ2 ≤ ... ≤ λp 指定。设 m < p 作为公因子的数量。估计因子载荷的矩阵是 p × m 矩阵,其中 L 的第 i列是  , i = 1, ..., m。
, i = 1, ..., m。
极大似然
极大似然法估计在假定数据遵循多变量正态分布时的因子载荷。由其名称便可以看出,此方法通过最大化与多变量正态模型相关的似然函数找到因子载荷和唯一方差的估计值。这也可以通过最小化涉及残差方差的表达式达到同样的效果。算法会进行迭代,直到找到最小值或达到最大的指定迭代数(默认为 25)。
Minitab 使用基于 Joreskog1、2的算法通过一些调整加强收敛。我们在这里对该算法做了简要小结。
假定我们有 p 个变量并且想要使用 m 个因子拟合模型。设 R 作为变量的 p × p 相关矩阵,设 L 作为因子载荷的 p × m 矩阵,设 Ψ 作为对角元素是唯一方差的 p × p 对角矩阵 Ψi。然后,我们需要找到最大化似然函数 f(L,Ψ) 的 L 和 Ψ 值。这涉及两个步骤,首先为 Ψ 找一个值,然后为 L 找一个值。
您可以间接地指定 Ψ 的初始值。在“因子分析 - 选项”子对话框中,输入包含使用初始公因子方差估计于中公因子方差初始值的列。Minitab 之后将 Ψ 对角元素计算为(1 − 公因子方差)。
对于 Ψ 的固定值,我们要相对于 L 最大化 f(L,Ψ)。这是一种简单的矩阵计算。之后将 L 的值代入 f(L,Ψ)。现在 f 可视为 Ψ 的函数。此函数的简单变换提供
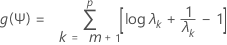
其中,λ1 < λ2 < ... λp 是 Ψ R- 1Ψ 的特征值。我们之后通过 Newton-Raphson 过程最小化 g(Ψ)。这得出 Ψ 的估计值,该值之后代入似然 f(L,Ψ)。然后,似然又一次相对于 L 进行最大化。计算出 g(Ψ) 的新值,以此类推。默认情况下,如果未达到收敛,迭代会继续多达 25 个步长。如果算法在 25 个步长中未达到收敛,您可能要在“选项”子对话框中更改默认的最大迭代次数。
如果下面任一项为真,则在第 n 个步长达到收敛:
- 函数 g(Ψ) 在连续性步长之间不会发生太大变化。具体地说,如果:
- | [第 n 个步长的 g(Ψ)] − [第 (n − 1) 个步长的 g(Ψ)] | < 10-6
- 所有唯一方差在连续性步长之间都不会发生太大变化。具体地说,如果:
- | ln(第 n 个步长的 Ψi)− ln(第 n − 1 个步长的 Ψi) | < K2,
对于所有 i = 1, ... , p,其中 Ψ 的第 i 个对角元素 Ψi 是对应于变量 i 的唯一方差。
K2 的值可在“选项”子对话框中的收敛中指定。默认情况下,该值为 0.005。
在“结果”子对话框中选择全部和最大似然提取迭代可显示每次迭代的信息。会显示目标函数 g(Ψ) 的值,之后在 ln(Ψi) 中发生最大变化。如果在一次迭代中,g(Ψ) 的值未减少,那么将采用较小(一半尺寸)的步长。继续半步直到 g(Ψ) 减少或采用 25 个半步。此时显示半步的数量。如果 g(Ψ) 在 25 个半步中未减少,则算法停止,并显示一条消息。
第二个导数的矩阵用于 g(Ψ) 的最小化。该矩阵并非总为正定。如果不是,则使用近似。当 Minitab 使用准确的矩阵时,结果中会出现星号。
最小化函数 g(Ψ) 时,可能发现 Ψ 的对角元素的值为 0 或为负。为防止出现这种情况,Minitab 的算法将 Ψ 的对角元素限制在 0 之外。具体地说,如果唯一方差 Ψi 小于 K2,则其设定为等于 K2。K2 是在“选项”子对话框中的“收敛”中设定的值。
当算法收敛时,会对唯一方差执行最终检查。如果任何一个唯一方差小于 K2,则它们设定为等于 0。对应的公因子方差则等于 1。此结果称为 Heywood 案例,并且 Minitab 会显示一条消息告知用户此结果。优化算法,比如用于极大似然因子分析的算法,可提供不同的答案,在输入中略有变化。例如,如果您更改了一些数据点、在使用初始公因子方差估计于中更改了初始值,或者在收敛中更改了收敛标准,您可能会发现因子分析结果出现差异。这对于解出现在极大似然曲面上相对平坦区域的情况尤为如此。
旋转载荷
正交旋转是因子载荷的正交转换,可让因子载荷的解释变得更容易。旋转载荷保留相关或协方差矩阵、残差矩阵、特殊方差和公因子方差。由于载荷发生变化,每个因子所占方差和相应的比率也会发生变化。
旋转将轴放置在接近尽可能多的点的位置并且将每个变量组与因子关联。但在一些情况下,变量接近不止一个轴,因此与不止一个因子关联。
可以从四种旋转方法中进行选择:
- 变量-因子方差最大法 - 使变量和因子中平方载荷的方差最大化。
- 因子方差最大法 - 使因子中平方载荷的方差最大化。这种方法简化了载荷矩阵的列并且是使用最广泛的旋转方法。为了使解释简单明了,此方法尝试将载荷变大或变小。
- 变量方差最大法 - 使变量中平方载荷的方差最大化。这种方法简化了载荷矩阵的行。
- 综合法指定 γ 值为 - 视参数 gamma 的值 (0 - 1) 而确定、由以上三种方法组成的旋转。
因子分析模型
因子分析模型如下:
X = μ + L F + e
其中,X 是测量值的 p x 1 向量、μ 是均值的 p x 1 向量、L 是载荷的 p × m 矩阵、F 是公因子的 m × 1 向量,以及 e 是残差的 p × 1 向量。在这里,p 表示主题或项目的测量次数,m 表示公因子数。F 和 e 假定为独立,各个 F 互相独立。F 和 e 的均值为 0、Cov(F) = I 为单位矩阵,Cov(e) = Ψ 为对角矩阵。关于 F 独立性的假定得到了这个正交因子模型。
在因子分析模型下,数据的 p × p 协方差矩阵 X 计算如下:
Cov(X) = L L' + Ψ
其中,L 是载荷的 p × m 矩阵并且 Ψ 是 p × p 对角矩阵。L L' 的第 i个对角元素,平方载荷之和,称为第 i个公因子方差。公因子方差值可评判为公因子解释的变异性百分比。Ψ 的第 i个对角元素称为第 i个特殊方差或唯一性。特殊方差指的是公因子未解释的变异性比率。公因子方差和/或特殊方差的大小可用来评估拟合的良好程度。
载荷
公式
使用主分量方法时,估计因子载荷的矩阵 L 通过以下公式提供:
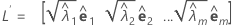
使用极大似然法时,因子载荷矩阵通过迭代过程获得。
表示法
| 项 | 说明 |
|---|---|
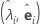 | 特征值-特征向量对 |
公因子方差
公式
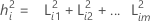
其中 i = 1, 2 ... p
表示法
| 项 | 说明 |
|---|---|
| L | 因子载荷矩阵 |
方差
由每个因子解释的数据变异性。如果使用主分量提取因子且不旋转载荷,则方差等于特征值。
方差贡献率
公式
使用相关矩阵时,第 j个因子解释的方差比率计算如下:
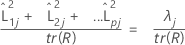
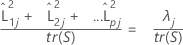
表示法
| 项 | 说明 |
|---|---|
| L | 因子载荷矩阵 |
| λj | 第 j个特征值 |
| tr(R) | 相关矩阵的跟踪 |
| tr(S) | 协方差矩阵的跟踪 |
系数
公式
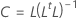
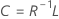
R 是相关矩阵。如果矩阵到因子是协方差矩阵,则 R 将被替换为协方差矩阵。
表示法
| 项 | 说明 |
|---|---|
| L | 因子载荷矩阵 |
分值
公式
F = ZC
表示法
| 项 | 说明 |
|---|---|
| F | 因子分值矩阵 |
| Z | 标准化数据 |
| C | 因子分值系数矩阵 |
