步骤 1:确定因子数
- 方差贡献率
- 使用方差贡献率 (% Var) 可确定因子解释的方差量。保留解释可接受方差水平的因子。可接受水平取决于您的应用。针对描述目的,可能只需解释 80% 的方差。但是,如果要对这些数据执行其他分析,则可能需要因子至少解释 90% 方差。
- 方差(特征值)
- 如果使用主分量提取因子,则方差等于特征值。可使用特征值的大小确定因子数。保留具有最大特征值的因子。例如,使用 Kaiser 标准时,仅使用特征值大于 1 的因子。
- 碎石图
- 碎石图按从大到小的顺序对特征值排序。理想图形趋势是一条陡曲线,后跟一段弯曲,然后是一条直线。使用陡曲线中在开始线趋势的第一个点之前的分量。
非旋转的载荷和公因子方差
| 变量 | 因子1 | 因子2 | 因子3 | 因子4 | 因子5 | 因子6 | 因子7 | 因子8 | 因子9 | 因子10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 学业成绩 | 0.726 | 0.336 | -0.326 | 0.104 | -0.354 | -0.099 | 0.233 | 0.147 | 0.097 | -0.142 |
| 外表 | 0.719 | -0.271 | -0.163 | -0.400 | -0.148 | -0.362 | -0.195 | -0.151 | 0.082 | 0.016 |
| 交流 | 0.712 | -0.446 | 0.255 | 0.229 | -0.319 | 0.119 | 0.032 | 0.088 | 0.023 | 0.204 |
| 个人与公司政策契合度 | 0.802 | -0.060 | 0.048 | 0.428 | 0.306 | -0.137 | -0.067 | 0.105 | -0.019 | -0.067 |
| 工作经验 | 0.644 | 0.605 | -0.182 | -0.037 | -0.092 | 0.317 | -0.209 | -0.102 | 0.121 | 0.039 |
| 工作契合度 | 0.813 | 0.078 | -0.029 | 0.365 | 0.368 | -0.067 | -0.025 | -0.032 | 0.146 | 0.066 |
| 求职信 | 0.625 | 0.327 | 0.654 | -0.134 | 0.031 | 0.025 | 0.017 | -0.113 | -0.079 | -0.130 |
| 亲和度 | 0.739 | -0.295 | -0.117 | -0.346 | 0.249 | 0.140 | 0.353 | -0.142 | 0.051 | 0.022 |
| 组织 | 0.706 | -0.540 | 0.140 | 0.247 | -0.217 | 0.136 | -0.080 | -0.105 | -0.020 | -0.162 |
| 潜力 | 0.814 | 0.290 | -0.326 | 0.167 | -0.068 | -0.073 | 0.048 | -0.112 | -0.290 | 0.100 |
| 简历 | 0.709 | 0.298 | 0.465 | -0.343 | -0.022 | -0.107 | 0.024 | 0.170 | 0.008 | 0.090 |
| 自信心 | 0.719 | -0.262 | -0.294 | -0.409 | 0.175 | 0.179 | -0.159 | 0.230 | -0.098 | -0.061 |
| 方差 | 6.3876 | 1.4885 | 1.1045 | 1.0516 | 0.6325 | 0.3670 | 0.3016 | 0.2129 | 0.1557 | 0.1379 |
| 方差贡献率 | 0.532 | 0.124 | 0.092 | 0.088 | 0.053 | 0.031 | 0.025 | 0.018 | 0.013 | 0.011 |
| 变量 | 因子11 | 因子12 | 公因子方差 |
|---|---|---|---|
| 学业成绩 | -0.026 | -0.031 | 1.000 |
| 外表 | 0.020 | -0.038 | 1.000 |
| 交流 | 0.012 | -0.100 | 1.000 |
| 个人与公司政策契合度 | 0.188 | -0.021 | 1.000 |
| 工作经验 | 0.077 | 0.009 | 1.000 |
| 工作契合度 | -0.176 | 0.008 | 1.000 |
| 求职信 | -0.043 | -0.127 | 1.000 |
| 亲和度 | 0.064 | 0.012 | 1.000 |
| 组织 | -0.032 | 0.136 | 1.000 |
| 潜力 | -0.023 | 0.028 | 1.000 |
| 简历 | 0.010 | 0.156 | 1.000 |
| 自信心 | -0.065 | -0.047 | 1.000 |
| 方差 | 0.0851 | 0.0750 | 12.0000 |
| 方差贡献率 | 0.007 | 0.006 | 1.000 |
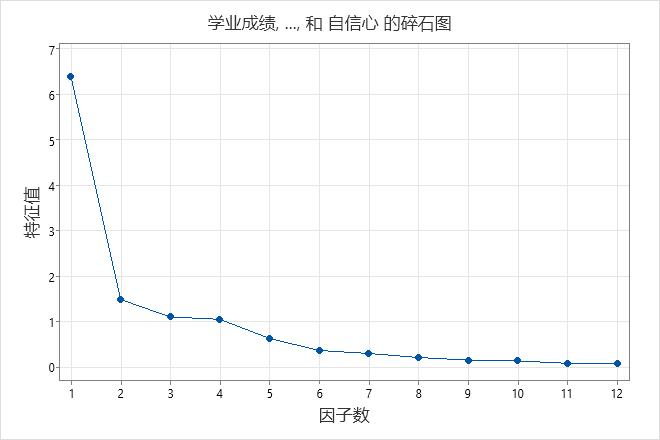
主要结果:方差贡献率、方差(特征值)、碎石图
这些结果显示使用主分量提取方法的所有因子的非旋转因子载荷。前四个因子的方差(特征值)大于 1。当使用超过 6 个因子时,特征值变化不那么明显。因此,4 到 6 个因子似乎可解释数据的大部分变异性。因子 1 解释的变异性百分比为 0.532 或 53.2%。因子 4 解释的变异性百分比为 0.088 或 8.8%。碎石图显示前四个因子在数据总变异性中占大多数比率。剩余的因子在变异性中所占比率非常小,并且可能不重要。
步骤 2:解释因子
确定因子数后(步骤 1),可使用极大似然法再次执行分析。然后,检查载荷模式,以确定对每个变量影响最强的因子。接近于 -1 或 1 的载荷表明因子对变量的影响非常强。接近于 0 的载荷表明因子对变量的影响很弱。有些变量可能对多个因子施加高载荷。
非旋转因子载荷通常很难解释。因子旋转简化了载荷结构,从而使您可以更容易地解释因子载荷。然而,没有哪种旋转方法在所有情况下都表现最佳。您可能想要尝试不同的旋转,并使用产生最佳解释结果的方法。还可以对旋转载荷排序,从而更为清楚地评估因子中的载荷。
旋转后的载荷和公因子方差
| 变量 | 因子1 | 因子2 | 因子3 | 因子4 | 公因子方差 |
|---|---|---|---|---|---|
| 学业成绩 | 0.481 | 0.510 | 0.086 | 0.188 | 0.534 |
| 外表 | 0.140 | 0.730 | 0.319 | 0.175 | 0.685 |
| 交流 | 0.203 | 0.280 | 0.802 | 0.181 | 0.795 |
| 个人与公司政策契合度 | 0.778 | 0.165 | 0.445 | 0.189 | 0.866 |
| 工作经验 | 0.472 | 0.395 | -0.112 | 0.401 | 0.553 |
| 工作契合度 | 0.844 | 0.209 | 0.305 | 0.215 | 0.895 |
| 求职信 | 0.219 | 0.052 | 0.217 | 0.947 | 0.994 |
| 亲和度 | 0.261 | 0.615 | 0.321 | 0.208 | 0.593 |
| 组织 | 0.217 | 0.285 | 0.889 | 0.086 | 0.926 |
| 潜力 | 0.645 | 0.492 | 0.121 | 0.202 | 0.714 |
| 简历 | 0.214 | 0.365 | 0.113 | 0.789 | 0.814 |
| 自信心 | 0.239 | 0.743 | 0.249 | 0.092 | 0.679 |
| 方差 | 2.5153 | 2.4880 | 2.0863 | 1.9594 | 9.0491 |
| 方差贡献率 | 0.210 | 0.207 | 0.174 | 0.163 | 0.754 |
主要结果:载荷、公因子方差、载荷图
- 适合公司 (0.778)、适合工作 (0.844) 和潜能 (0.645) 在因子 1 上具有较大的正载荷,因此该因子描述员工适合度以及在公司的成长潜力。
- 相貌 (0.73)、受欢迎度 (0.615) 和自信心 (0.743) 在因子 2 上具有较大的正载荷,因此该因子描述个人才能。
- 沟通能力 (0.802) 和组织能力 (0.889) 在因子 3 上具有较大的正载荷,因此该因子描述工作技能。
- 信件 (0.947) 和简历 (0.789) 在因子 4 上具有较大的正载荷,因此该因子描述写作技能。
所有这四个因子共同解释数据变异的 0.754 或 75.4%。
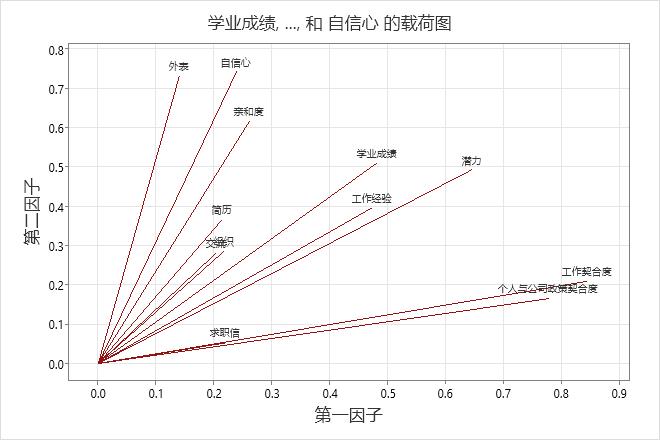
载荷图可直观地显示前两个因子的载荷结果。
步骤 3:检查数据是否有问题
如果前两个因子在数据变异中占大部分比率,则可以使用分值图评估数据结构并检测聚类、异常值和趋势。该图的数据分组情况可以说明数据中两种或两种以上不同的分布。如果数据遵循正态分布,并且不存在异常值,则这些点将随机分布在值 0 的周围。
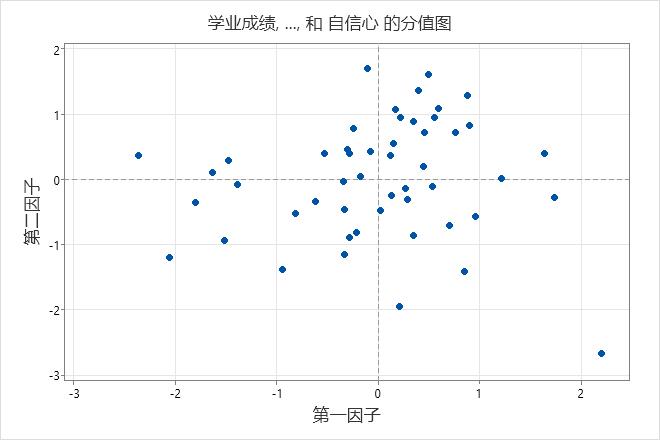
主要结果:分值图
在此分值图中,数据显示为正态,没有明显的异常值。但是,您可能想要调查此图右下角中显示的数据值,该值与其他数据值相距较远。
提示
要查看每个观测值的计算分值,请将指针放在图形中数据点之上。要为其他因子创建分值图,请存储分值并使用。
