因子载荷
因子载荷表示因子对变量的解释程度。载荷范围可以为 -1 到 1。
如果您为分析选择旋转方法,Minitab 会计算非旋转因子载荷和旋转因子载荷。
解释
检查载荷模式,以确定对每个变量影响最强的因子。接近于 -1 或 1 的载荷表明因子对变量的影响非常强。接近于 0 的载荷表明因子对变量的影响很弱。有些变量可能对多个因子施加高载荷。
非旋转因子载荷通常很难解释。因子旋转简化了载荷结构,并且使因子更容易辨识和解释。然而,没有哪种旋转方法在所有情况下都表现最佳。您可能想要尝试不同的旋转,并使用产生最佳解释结果的旋转。您还可以对旋转载荷排序,从而更为清楚地评估因子中的载荷。
- 适合公司 (0.778)、适合工作 (0.844) 和潜能 (0.645) 在因子 1 上具有较大的正载荷,因此该因子描述员工适合度以及在公司的成长潜力。
- 相貌 (0.73)、受欢迎度 (0.615) 和自信心 (0.743) 在因子 2 上具有较大的正载荷,因此该因子描述个人才能。
- 沟通能力 (0.802) 和组织能力 (0.889) 在因子 3 上具有较大的正载荷,因此该因子描述工作技能。
- 信件 (0.947) 和简历 (0.789) 在因子 4 上具有较大的正载荷,因此该因子描述写作技能。
非旋转的载荷和公因子方差
| 变量 | 因子1 | 因子2 | 因子3 | 因子4 | 公因子方差 |
|---|---|---|---|---|---|
| 学业成绩 | 0.380 | 0.455 | 0.340 | 0.259 | 0.534 |
| 外表 | 0.359 | 0.530 | -0.040 | 0.523 | 0.685 |
| 交流 | 0.465 | 0.660 | -0.377 | -0.023 | 0.795 |
| 个人与公司政策契合度 | 0.523 | 0.677 | 0.266 | -0.253 | 0.866 |
| 工作经验 | 0.508 | 0.194 | 0.450 | 0.232 | 0.553 |
| 工作契合度 | 0.532 | 0.632 | 0.415 | -0.201 | 0.895 |
| 求职信 | 0.992 | -0.094 | -0.012 | -0.007 | 0.994 |
| 亲和度 | 0.412 | 0.529 | 0.032 | 0.377 | 0.593 |
| 组织 | 0.406 | 0.761 | -0.424 | -0.055 | 0.926 |
| 潜力 | 0.446 | 0.548 | 0.431 | 0.172 | 0.714 |
| 简历 | 0.850 | 0.040 | 0.096 | 0.283 | 0.814 |
| 自信心 | 0.293 | 0.575 | 0.083 | 0.506 | 0.679 |
| 方差 | 3.6320 | 3.3193 | 1.0883 | 1.0095 | 9.0491 |
| 方差贡献率 | 0.303 | 0.277 | 0.091 | 0.084 | 0.754 |
旋转后的载荷和公因子方差
| 变量 | 因子1 | 因子2 | 因子3 | 因子4 | 公因子方差 |
|---|---|---|---|---|---|
| 学业成绩 | 0.481 | 0.510 | 0.086 | 0.188 | 0.534 |
| 外表 | 0.140 | 0.730 | 0.319 | 0.175 | 0.685 |
| 交流 | 0.203 | 0.280 | 0.802 | 0.181 | 0.795 |
| 个人与公司政策契合度 | 0.778 | 0.165 | 0.445 | 0.189 | 0.866 |
| 工作经验 | 0.472 | 0.395 | -0.112 | 0.401 | 0.553 |
| 工作契合度 | 0.844 | 0.209 | 0.305 | 0.215 | 0.895 |
| 求职信 | 0.219 | 0.052 | 0.217 | 0.947 | 0.994 |
| 亲和度 | 0.261 | 0.615 | 0.321 | 0.208 | 0.593 |
| 组织 | 0.217 | 0.285 | 0.889 | 0.086 | 0.926 |
| 潜力 | 0.645 | 0.492 | 0.121 | 0.202 | 0.714 |
| 简历 | 0.214 | 0.365 | 0.113 | 0.789 | 0.814 |
| 自信心 | 0.239 | 0.743 | 0.249 | 0.092 | 0.679 |
| 方差 | 2.5153 | 2.4880 | 2.0863 | 1.9594 | 9.0491 |
| 方差贡献率 | 0.210 | 0.207 | 0.174 | 0.163 | 0.754 |
公因子方差
公因子方差是由因子解释的每个变量的变异性比率。无论您为分析使用非旋转因子载荷还是旋转因子载荷,公因子方差值都是相同的。
解释
检查公因子方差值以评估因子对每个变量的解释程度。公因子方差越接近于 1,因子对变量的解释程度越好。如果因子对某些变量的拟合有重大影响,则可以决定添加因子。
非旋转的载荷和公因子方差
| 变量 | 因子1 | 因子2 | 因子3 | 因子4 | 公因子方差 |
|---|---|---|---|---|---|
| 学业成绩 | 0.380 | 0.455 | 0.340 | 0.259 | 0.534 |
| 外表 | 0.359 | 0.530 | -0.040 | 0.523 | 0.685 |
| 交流 | 0.465 | 0.660 | -0.377 | -0.023 | 0.795 |
| 个人与公司政策契合度 | 0.523 | 0.677 | 0.266 | -0.253 | 0.866 |
| 工作经验 | 0.508 | 0.194 | 0.450 | 0.232 | 0.553 |
| 工作契合度 | 0.532 | 0.632 | 0.415 | -0.201 | 0.895 |
| 求职信 | 0.992 | -0.094 | -0.012 | -0.007 | 0.994 |
| 亲和度 | 0.412 | 0.529 | 0.032 | 0.377 | 0.593 |
| 组织 | 0.406 | 0.761 | -0.424 | -0.055 | 0.926 |
| 潜力 | 0.446 | 0.548 | 0.431 | 0.172 | 0.714 |
| 简历 | 0.850 | 0.040 | 0.096 | 0.283 | 0.814 |
| 自信心 | 0.293 | 0.575 | 0.083 | 0.506 | 0.679 |
| 方差 | 3.6320 | 3.3193 | 1.0883 | 1.0095 | 9.0491 |
| 方差贡献率 | 0.303 | 0.277 | 0.091 | 0.084 | 0.754 |
在这些结果中,从 12 个变量中提取了 4 个因子。所有变量的公因子方差值通常比较高,这说明 4 个因子充分表示变量。例如,适合工作中 0.895 或 89.5% 的变异性都由这 4 个因子来解释。
方差
由每个因子解释的数据变异性。如果使用主分量提取方法且不旋转载荷,则每个因子的方差等于特征值。虽然所有因子解释的总变异保持不变,但旋转会改变每个因子解释的变异比率的分布。
解释
检查每个因子的方差。方差越高,表明因子解释的数据变异性所占比率也越高。如果不知道要在分析中提取多少因子,请先使用主分量提取方法且不旋转,将默认因子数(提取的最大因子数)作为初步评估。然后,将重要因子定义为方差(特征值)大于特定值的因子。例如,一项标准是包括特征值至少为 1 的任何因子。另一种方法是直观地评估碎石图上的特征值,以确定特征值在哪个点显示的变化不大并且接近 0。有关更多信息,请参见有关碎石图的主题。
非旋转的载荷和公因子方差
| 变量 | 因子1 | 因子2 | 因子3 | 因子4 | 因子5 | 因子6 | 因子7 | 因子8 | 因子9 | 因子10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 学业成绩 | 0.726 | 0.336 | -0.326 | 0.104 | -0.354 | -0.099 | 0.233 | 0.147 | 0.097 | -0.142 |
| 外表 | 0.719 | -0.271 | -0.163 | -0.400 | -0.148 | -0.362 | -0.195 | -0.151 | 0.082 | 0.016 |
| 交流 | 0.712 | -0.446 | 0.255 | 0.229 | -0.319 | 0.119 | 0.032 | 0.088 | 0.023 | 0.204 |
| 个人与公司政策契合度 | 0.802 | -0.060 | 0.048 | 0.428 | 0.306 | -0.137 | -0.067 | 0.105 | -0.019 | -0.067 |
| 工作经验 | 0.644 | 0.605 | -0.182 | -0.037 | -0.092 | 0.317 | -0.209 | -0.102 | 0.121 | 0.039 |
| 工作契合度 | 0.813 | 0.078 | -0.029 | 0.365 | 0.368 | -0.067 | -0.025 | -0.032 | 0.146 | 0.066 |
| 求职信 | 0.625 | 0.327 | 0.654 | -0.134 | 0.031 | 0.025 | 0.017 | -0.113 | -0.079 | -0.130 |
| 亲和度 | 0.739 | -0.295 | -0.117 | -0.346 | 0.249 | 0.140 | 0.353 | -0.142 | 0.051 | 0.022 |
| 组织 | 0.706 | -0.540 | 0.140 | 0.247 | -0.217 | 0.136 | -0.080 | -0.105 | -0.020 | -0.162 |
| 潜力 | 0.814 | 0.290 | -0.326 | 0.167 | -0.068 | -0.073 | 0.048 | -0.112 | -0.290 | 0.100 |
| 简历 | 0.709 | 0.298 | 0.465 | -0.343 | -0.022 | -0.107 | 0.024 | 0.170 | 0.008 | 0.090 |
| 自信心 | 0.719 | -0.262 | -0.294 | -0.409 | 0.175 | 0.179 | -0.159 | 0.230 | -0.098 | -0.061 |
| 方差 | 6.3876 | 1.4885 | 1.1045 | 1.0516 | 0.6325 | 0.3670 | 0.3016 | 0.2129 | 0.1557 | 0.1379 |
| 方差贡献率 | 0.532 | 0.124 | 0.092 | 0.088 | 0.053 | 0.031 | 0.025 | 0.018 | 0.013 | 0.011 |
| 变量 | 因子11 | 因子12 | 公因子方差 |
|---|---|---|---|
| 学业成绩 | -0.026 | -0.031 | 1.000 |
| 外表 | 0.020 | -0.038 | 1.000 |
| 交流 | 0.012 | -0.100 | 1.000 |
| 个人与公司政策契合度 | 0.188 | -0.021 | 1.000 |
| 工作经验 | 0.077 | 0.009 | 1.000 |
| 工作契合度 | -0.176 | 0.008 | 1.000 |
| 求职信 | -0.043 | -0.127 | 1.000 |
| 亲和度 | 0.064 | 0.012 | 1.000 |
| 组织 | -0.032 | 0.136 | 1.000 |
| 潜力 | -0.023 | 0.028 | 1.000 |
| 简历 | 0.010 | 0.156 | 1.000 |
| 自信心 | -0.065 | -0.047 | 1.000 |
| 方差 | 0.0851 | 0.0750 | 12.0000 |
| 方差贡献率 | 0.007 | 0.006 | 1.000 |
此分析使用主分量方法和默认设置(无旋转)执行。前四个因子的方差(特征值)大于 1。当使用超过 6 个因子时,特征值变化不那么明显。因此,4 个因子解释大部分数据变异性。基于这些初步结果,再次执行因子分析并仅提取 4 个因子,然后采用不同旋转进行试验。
方差贡献率
方差贡献率 (% Var) 指的是由每个因子解释的数据变异性的比率。方差贡献率的值范围可以为 0 (0%) 到 1 (100%)。
解释
检查每个因子的方差贡献率值。方差贡献率值越高表明因子解释的变异性越多。因此,您可以使用方差贡献率值确定哪些因子最重要。
方差贡献率的公因子方差值表示分析中所有因子解释的总变异。使用此值可帮助确定分析中使用的因子数是否解释数据中足够量的总变异。
非旋转的载荷和公因子方差
| 变量 | 因子1 | 因子2 | 因子3 | 因子4 | 公因子方差 |
|---|---|---|---|---|---|
| 学业成绩 | 0.380 | 0.455 | 0.340 | 0.259 | 0.534 |
| 外表 | 0.359 | 0.530 | -0.040 | 0.523 | 0.685 |
| 交流 | 0.465 | 0.660 | -0.377 | -0.023 | 0.795 |
| 个人与公司政策契合度 | 0.523 | 0.677 | 0.266 | -0.253 | 0.866 |
| 工作经验 | 0.508 | 0.194 | 0.450 | 0.232 | 0.553 |
| 工作契合度 | 0.532 | 0.632 | 0.415 | -0.201 | 0.895 |
| 求职信 | 0.992 | -0.094 | -0.012 | -0.007 | 0.994 |
| 亲和度 | 0.412 | 0.529 | 0.032 | 0.377 | 0.593 |
| 组织 | 0.406 | 0.761 | -0.424 | -0.055 | 0.926 |
| 潜力 | 0.446 | 0.548 | 0.431 | 0.172 | 0.714 |
| 简历 | 0.850 | 0.040 | 0.096 | 0.283 | 0.814 |
| 自信心 | 0.293 | 0.575 | 0.083 | 0.506 | 0.679 |
| 方差 | 3.6320 | 3.3193 | 1.0883 | 1.0095 | 9.0491 |
| 方差贡献率 | 0.303 | 0.277 | 0.091 | 0.084 | 0.754 |
在这些结果中,数据变异性的 0.303 或 30.3% 由因子 1 解释。这四个因子共同解释数据中 0.754 或 75.4% 的变异性。
因子分值系数
在因子分析中,因子系数标识分量中每个变量的相对权重。系数的绝对值越大,对应变量在计算分量时就越重要。Minitab 使用因子系数计算因子分值,分值是因子的估计值。Minitab 计算因子分值的方法是,将因子分值系数(列在因子 1、因子 2 等的下方)与通过减去均值以尺规化和中心化的数据相乘。
解释
- 检查观测值的行为。
- 用于其他分析,例如回归分析或多元方差分析。
注意
必须标准化变量,以使用估计的系数计算因子分值。
碎石图
碎石图显示因子数与对应的特征值。碎石图按从最大到最小的顺序排列特征值。未旋转时,相关矩阵的特征值等于因子的方差。
要显示碎石图,您必须单击图形并在执行分析时选择碎石图。
解释
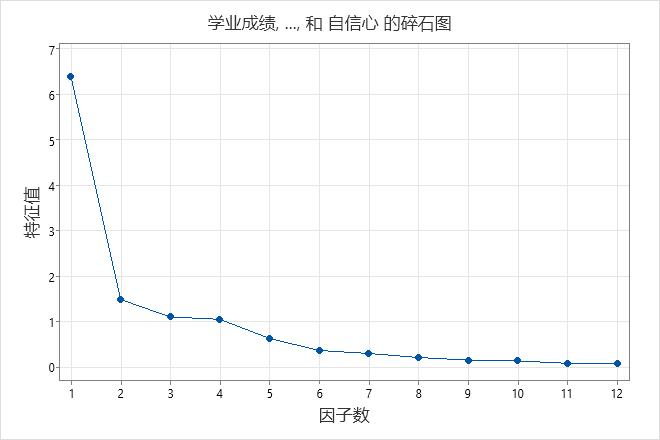
此碎石图显示前四个因子在数据(由特征值提供)总变异性中占大部分比率。前四个因子的特征值均大于 1。剩余的因子在变异性中所占比率非常小,并且可能不重要。
分值图
分值图相对于第一因子分值绘制第二因子分值。
要显示分值图,必须单击图形并在执行分析时选择分值图。
解释
如果前两个因子在数据变异中占大部分比率,则可以使用分值图评估数据结构并检测聚类、异常值和趋势。该图的数据分组情况可以说明数据中两种或两种以上不同的分布。如果数据遵循正态分布,并且不存在异常值,则这些点将随机分布在值 0 的周围。
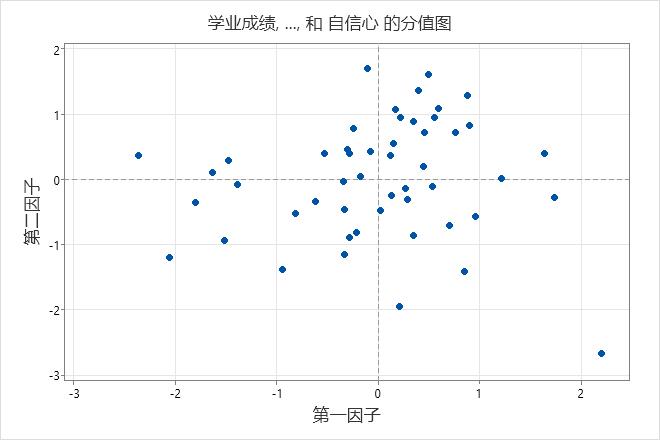
在此分值图中,数据显示为正态,没有明显的异常值。但是,您可能想要调查此图右下角中显示的数据值,该值与其他数据值相距较远。
提示
要查看每个观测值的计算分值,请将指针放在图形中数据点之上。要为其他因子创建分值图,请存储分值并使用。
载荷图
载荷图相对于第二个因子的旋转因子载荷绘制第一个因子各变量的旋转因子载荷。
要显示载荷图,必须单击图形,并在执行分析时选择载荷图。
解释
使用载荷图可标识哪些变量对因子的影响最强。载荷范围可以为 -1 到 1。接近于 -1 或 1 的载荷表明变量对因子的影响非常强。接近于 0 的载荷表明变量对因子的影响很弱。评估载荷还可帮助您根据变量表示每个因子的特征。选择因子数后,请尝试不同的旋转,以便更轻松地解释因子载荷。
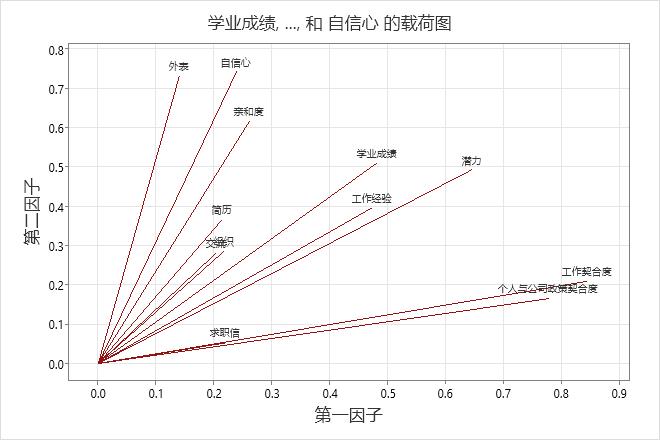
对于此载荷图,对数据执行了因子方差最大法旋转,这使得前两个因子更容易解释。适合工作和适合公司在因子 1 上具有较大的正载荷,因此该因子描述求职者对该职位的适合度。相貌、受欢迎度和自信心在因子 2 上具有较大的正载荷,因此该因子描述求职者的个人才能。
双标图
双标图与分值图和载荷图重叠。
要显示双标图,必须单击图形,并在执行分析时选择双标图。
解释
使用双标图可在一个图形中评估前两个因子的数据结构和载荷。Minitab 相对于第一个因子分值绘制第二个因子分值以及这两个因子的载荷。
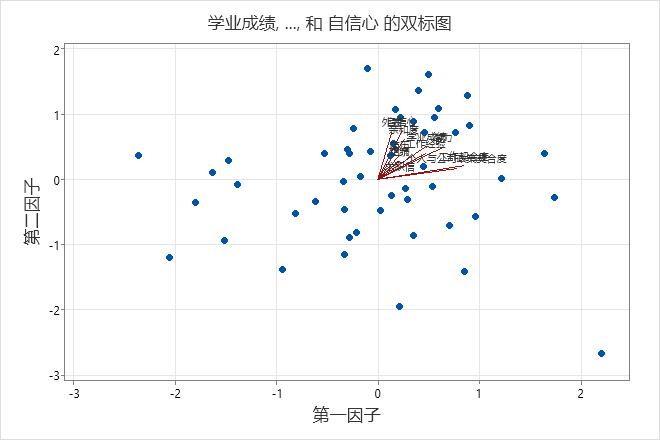
- 数据显示为正态,没有极端异常值。但是,您可能想要调查此图右下角中显示的数据值,该值与其他数据值相距较远。
- 适合工作和适合公司在因子 1 上具有较大的正载荷,因此该因子描述求职者对该职位的适合度。
- 相貌、受欢迎度和自信心在因子 2 上具有较大的正载荷,因此该因子描述求职者的个人才能。
