平方距离
平方 Mahalanobis 距离 - 一般形式
线性判别的观测值 x 到组 t 中心(均值)的平方距离(亦称为 Mahalanobis 距离)通过以下一般形式提供:

平方 Mahalanobis 距离 - 二次函数
二次判别函数的 x 到组 t 的平方 Mahalanobis 距离计算如下:

广义平方距离 - 线性函数
线性判别函数的 x 到组 t 的广义平方距离计算如下:
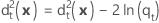
广义平方距离 - 二次函数
二次判别函数的 x 到组 t 的广义平方距离计算如下:

后验概率
属于组 t 的 x 后验概率计算如下:
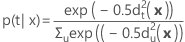
线性判别分值
线性判别分值计算如下:

表示法
| 项 | 说明 |
|---|---|
| x | 包含此观测值的预测变量值的长度 p 的列向量(此列向量存储为一行) |
| p | 预测变量数 |
| n | 观测值总数 |
| t | 组下标 |
| nt | 组 t 中的观测值个数 |
| qt | 组 t 的先验概率,其等于 nt/n |
| Sp | 用于线性判别分析的合并协方差矩阵 |
| Si | 用于二次判别分析的组 i 的协方差矩阵 |
| mt | 包含根据组 t 中数据计算的预测变量均值的长度 p 的列向量 |
| St | 组 t 的协方差矩阵 |
| |St| | St 的行列式 |
线性判别函数
线性判别函数对应于多元回归中的回归系数,计算如下:


对于给定的 x,此规则将 x 分配给具有最大线性判别函数的组。
表示法
| 项 | 说明 |
|---|---|
| x | 包含此观测值预测变量值的长度 p 的列向量(此列向量存储为一行) |
| mi | 包含根据组 i 中数据计算的预测变量均值的长度 p 的列向量 |
| Sp | 合并协方差矩阵 |
| ln pi | 组 i 的先验概率的自然对数 |
广义平方距离
广义平方距离用作二次距离度量,计算如下:


表示法
| 项 | 说明 |
|---|---|
| x | 包含此观测值预测变量值的长度 p 的列向量(此列向量存储为一行) |
| mi | 包含根据组 i 中数据计算的预测变量均值的长度 p 的列向量 |
| Sp | 合并协方差矩阵 f |
| In pi | 组 i 的先验概率的自然对数 |
后验概率
后验概率是给定数据并按以下方式计算的组 i 的概率:
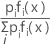
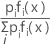
最大后验概率等于 In [pi fi (x)] 的最大值
其中(如果分布是正态的):


并且


表示法
| 项 | 说明 |
|---|---|
| pi | 组 i 的先验概率 |
| fi(x) | 组 i 中数据的联合密度(用样本估计值替换了总体参数) |
