步骤 1:检查相似性和距离水平
在合并过程的每一步,查看形成的聚类并检查其相似性水平和距离水平。相似性水平越高,每个聚类中的变量越相似(相关)。距离水平越低,每个聚类中的变量越靠近。
理想情况下,聚类应具有相对较高的相似性水平和相对较低的距离水平。但是,必须设定合理且实际的聚类数,来平衡该目标。
合并步骤
| 步骤 | 点群数 | 相似性水平 | 距离水平 | 已合并的点群号 | 新聚类号 | 新聚类号中的观测值个数 | |
|---|---|---|---|---|---|---|---|
| 1 | 4 | 93.9666 | 0.120669 | 2 | 3 | 2 | 2 |
| 2 | 3 | 93.1548 | 0.136904 | 4 | 5 | 4 | 2 |
| 3 | 2 | 87.3150 | 0.253700 | 1 | 4 | 1 | 3 |
| 4 | 1 | 79.8113 | 0.403775 | 1 | 2 | 1 | 5 |
主要结果:相似性水平、距离水平
在这些结果中,数据总共包含 5 个变量。在步骤 1 中,两个聚类(工作表中的变量 2 和 3)合并形成新聚类。这在数据中创建 4 个聚类,其相似性水平为 93.9666、距离水平为 0.130669。尽管相似性水平较高、距离水平较低,聚类数还是过高,因此用处不大。在每个后续步骤,随着新聚类的形成,相似性水平会降低、距离水平就增加。在最后一步,所有变量合并成一个聚类。
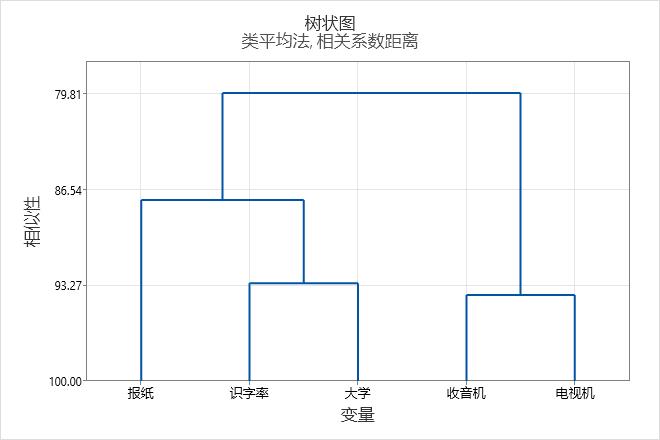
要查看树状图中的相似性水平,请将鼠标指针放在 Minitab 的树状图中的水平线上。
步骤 2:确定数据的最终分组
使用在每一步合并的聚类的相似性水平可帮助确定数据的最终分组。注意步骤之间相似性水平出现的突变。在相似性发生突变之前的步骤可为最终分割提供良好的分界点。对于最终分割,聚类应保持相对较高的相似性水平。您还应运用自己的实践性数据知识来确定对于您的应用最有意义的最终分组。
例如,以下合并表显示相似性水平从步骤 1 (93.9666) 到步骤 2 (93.1548) 略微下降。然后,当聚类数从 3 变为 2 时,该相似性在步骤 3 (87.3150) 骤减。这些结果表明 3 个聚类可能适合最终分割。如果此分组具有直观意义,则这可能是个不错的选择。
合并步骤
| 步骤 | 点群数 | 相似性水平 | 距离水平 | 已合并的点群号 | 新聚类号 | 新聚类号中的观测值个数 | |
|---|---|---|---|---|---|---|---|
| 1 | 4 | 93.9666 | 0.120669 | 2 | 3 | 2 | 2 |
| 2 | 3 | 93.1548 | 0.136904 | 4 | 5 | 4 | 2 |
| 3 | 2 | 87.3150 | 0.253700 | 1 | 4 | 1 | 3 |
| 4 | 1 | 79.8113 | 0.403775 | 1 | 2 | 1 | 5 |
主要结果:相似性水平、聚类数

有关最终分组的决定又称为切割树状图。切割树状图类似于在树状图中画水平线指定最终分组。例如,要将树状图切割成四个聚类,想象在垂直轴的中间位置向下(正好在相似性水平约 88 之下)画一条水平线。
步骤 3:检查最终分割
在步骤 2 中确定最终分组后,重复执行分析并指定最终分割的聚类数(或相似性水平)。此时,Minitab 会显示最终分割表格,其中显示形成最终分割中每个聚类的变量。
检查最终分割中的聚类,以确定分组是否合乎您应用的逻辑。如果您仍不确定,请重复执行该分析,并且比较不同最终分组的树状图,以确定最合乎数据逻辑的最终分组。
合并步骤
| 步骤 | 点群数 | 相似性水平 | 距离水平 | 已合并的点群号 | 新聚类号 | 新聚类号中的观测值个数 | |
|---|---|---|---|---|---|---|---|
| 1 | 4 | 93.9666 | 0.120669 | 2 | 3 | 2 | 2 |
| 2 | 3 | 93.1548 | 0.136904 | 4 | 5 | 4 | 2 |
| 3 | 2 | 87.3150 | 0.253700 | 1 | 4 | 1 | 3 |
| 4 | 1 | 79.8113 | 0.403775 | 1 | 2 | 1 | 5 |
最终分割
| 变量 | |
|---|---|
| 聚类 1 | 报纸 |
| 聚类 2 | 收音机 电视机 |
| 聚类 3 | 识字率 大学 |
主要结果:最终分割、树状图
在这些结果中,最终分割中形成了三个聚类:
- 每 1,000 人的报纸份数
- 收音机和电视机数
- 文化程度以及城市是否设有大学
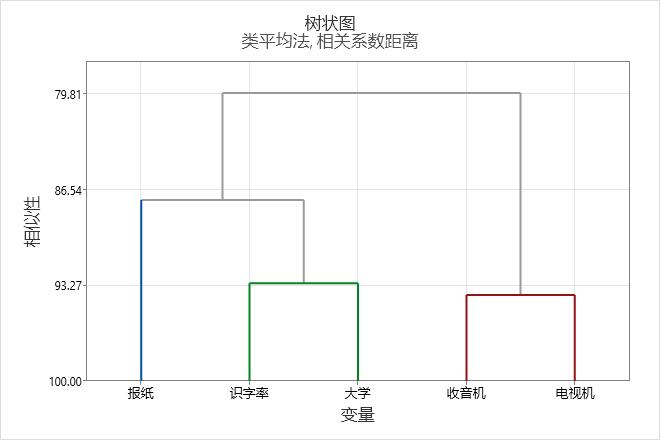
此树状图使用 3 个聚类的最终分割而创建。每个最终聚类用不同的颜色表示。树状图在大约 88 的相似性水平处切割。如果您切割树状图的高度越高,最终聚类将越少,但相似性水平将降低。如果您切割树状图的高度越低,相似性水平将越高,但最终聚类将越多。
