步骤
联结聚类的合并过程中的步骤数。在每个步骤,新聚类与现有聚类联结,并且会计算它们的相似性水平和距离水平。
聚类数
在合并过程中的每步形成的聚类数。开始第一步前,聚类数等于观测值(观测值聚类)总数或变量(变量聚类)总数。在第一步中,两个聚类合并形成一个新聚类。在后续每步,另一个聚类与现有聚类合并形成一个新聚类。在最后一步,所有观测值或变量合并成一个聚类。
可以在主对话框中输入聚类数,以指定数据的最终分割。所选的联结法和距离度量将显著影响聚类结果。
相似性水平
每个合并步骤的聚类之间最小距离相对于数据中最大观测值内距离的百分比。两个聚类 i 和 j 之间的相似性 s(ij) 计算公式为:s(ij) = 100 * [1 - d(ij)) / d(max)],其中 d(max) 是原始距离矩阵 D 中的最大值,条目 d(ij) 是 i 和 j 之间的距离。
解释
使用在每一步合并的聚类的相似性水平可帮助确定数据的最终分组。注意步骤之间相似性水平出现的突变。在相似性发生突变之前的步骤可为最终分割提供良好的分界点。对于最终分割,聚类应保持相对较高的相似性水平。您还应运用自己的实践性数据知识来确定对于您的应用最有意义的最终分组。
例如,以下合并表显示相似性水平从步骤 1 (93.9666) 到步骤 2 (93.1548) 略微下降。然后,当聚类数从 3 变为 2 时,该相似性在步骤 3 (87.3150) 骤减。这些结果表明 3 个聚类可能适合最终分割。如果此分组具有直观意义,则这可能是个不错的选择。
合并步骤
| 步骤 | 点群数 | 相似性水平 | 距离水平 | 已合并的点群号 | 新聚类号 | 新聚类号中的观测值个数 | |
|---|---|---|---|---|---|---|---|
| 1 | 4 | 93.9666 | 0.120669 | 2 | 3 | 2 | 2 |
| 2 | 3 | 93.1548 | 0.136904 | 4 | 5 | 4 | 2 |
| 3 | 2 | 87.3150 | 0.253700 | 1 | 4 | 1 | 3 |
| 4 | 1 | 79.8113 | 0.403775 | 1 | 2 | 1 | 5 |
距离水平
在每步合并的聚类(使用所选的联结法)或变量(使用所选的距离度量)之间的距离。Minitab 会基于联结法和您在主对话框中选择的距离度量计算距离水平。
两个变量之间的距离与其相关性直接相关。即,对于两个变量 X1 和 X2,距离等于 1− 相关。例如,如果 Corr(X1,X2) = 0.879,则距离 (X1,X2) = 1 − 0.879 = 0.121。
解释
使用在每步合并的聚类的距离水平可帮助确定数据的最终分组。注意步骤之间距离水平出现的突变。在发生距离突变之前的步骤为最终分割提供良好的分界点。对于最终分割,聚类应保持相对小的距离水平。您还应运用自己的实践性数据知识来确定对于您的应用最有意义的最终分组。
例如,下列合并表显示距离水平从步骤 1 (0.120669) 到步骤 2 (0.136904) 略微增加。当聚类数从 3 变为 2 时,该距离在步骤 3 (0.253700) 突增。这些结果表明 3 个聚类可能适合最终分割。如果此分组具有直观意义,则这可能是个不错的选择。
合并步骤
| 步骤 | 点群数 | 相似性水平 | 距离水平 | 已合并的点群号 | 新聚类号 | 新聚类号中的观测值个数 | |
|---|---|---|---|---|---|---|---|
| 1 | 4 | 93.9666 | 0.120669 | 2 | 3 | 2 | 2 |
| 2 | 3 | 93.1548 | 0.136904 | 4 | 5 | 4 | 2 |
| 3 | 2 | 87.3150 | 0.253700 | 1 | 4 | 1 | 3 |
| 4 | 1 | 79.8113 | 0.403775 | 1 | 2 | 1 | 5 |
已合并的聚类
在合并过程中的每步通过合并形成新聚类的两个聚类。
新聚类
在合并过程中的每步形成的新聚类的标识号。新聚类的标识号始终是已合并的两个聚类的标识号中较小的那个。例如,如果聚类 2 和聚类 9 合并,则形成的新聚类称为聚类 2。
新聚类中的观测值个数
在合并过程中的每一步形成的每个新聚类的观测值个数。在最后一步,所有观测值合并成一个聚类。因此,最后一步形成的新聚类中的观测值个数等于数据中的观测值总数。
注意
对于变量聚类,观测值个数为新聚类中的变量数。
最终分割
如果您在主对话框中指定最终分割,Minitab 会显示各个聚类中变量的列表。根据您的特定应用,最终分割中每个聚类内的变量应具有直观意义。
树状图
树状图显示每步通过聚类变量形成的组及其相似性水平。默认情况下,沿垂直轴测量相似性水平(或者,可以显示距离水平),而沿水平轴列出不同的变量。
解释
使用树状图可查看这些聚类在各步如何形成,并且评估所形成聚类的相似性(或距离)水平。
要查看相似性(或距离)水平,请将鼠标指针放在树状图中的水平线上。相似性或距离值随步骤变化的模式可以帮助您选择数据的最终分组。值发生突变的步骤可能是定义最终分组的合适点。
有关最终分组的决定又称为切割树状图。切割树状图类似于在树状图中画线以指定最终分组。还可以比较不同最终分组的树状图,帮助您确定对数据最有意义的分组。
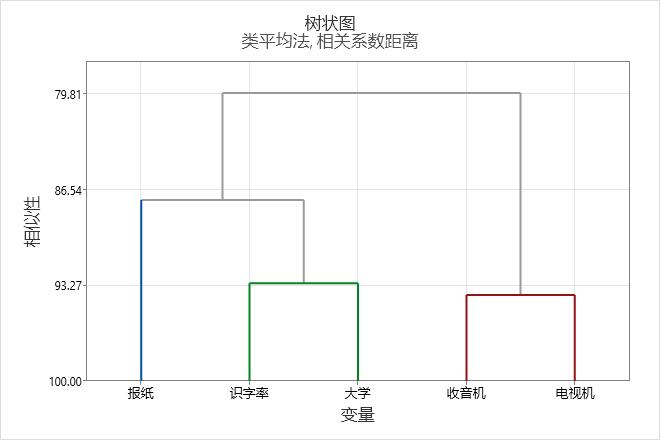
此树状图使用 3 个聚类的最终分割而创建。每个最终聚类用不同的颜色表示。树状图在大约 88 的相似性水平处“切割”。如果您切割树状图的高度越高,最终聚类将越少,但相似性水平将降低。如果您切割树状图的高度越低,相似性水平将越高,但最终聚类将越多。
注意
对于一些数据集,平均法、质心法、中位数法和 Ward 法可能不会生成分层树状图。也就是说,合并距离并非总在每步增加。在树状图中,这一步产生的合并将会向下而不是向上。
