社会科学家想要研究媒体渠道和大学数以及文化程度对全城大学录取人数的影响。对于全世界 10 个城市,科学家将确定每 1,000 人所拥有的报纸份数、收音机数和电视机数。他还会记录文化程度以及每个城市是否设有大学。科学家想通过按相似特征合并变量来减少变量的总数。
- 打开样本数据集,大学录取.MWX。
- 选择。
- 在变量或距离矩阵中,输入报纸收音机 '电视机' '识字率' 大学。
- 从联结法中,选择平均。
- 在距离度量下,选择相关性。
- 选择显示树状图。
- 单击确定。
解释结果
该表格显示每步合并的聚类、聚类之间的距离和聚类的相似性。
- 相似性水平从步骤 1 (93.9666) 到步骤 2 (93.1548) 略微下降。然后,当聚类数从 3 变为 2 时,该相似性在步骤 3 (87.3150) 突减。
- 合并聚类之间的距离从步骤 1 到步骤 2 略微增加约 0.017。然后,当聚类数从 3 变为 2 时,该距离在步阶 3 突增。
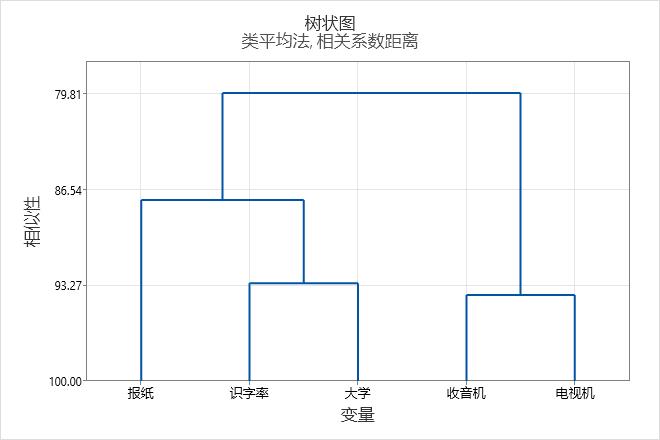
距离和相似性结果表明 3 个聚类对于最终分割是足够的。如果社会科学家认为此分组具有直观意义,则这可能是个不错的选择。树状图以树形图的形式显示表格中的信息。
社会科学家应重新运行分析,并在最终分割中指定 3 个聚类。当您指定最终分割时,Minitab 会显示附加的表格,描述最终分割中包含的每个聚类的特征。
相关系数距离, 类平均法
合并步骤
| 步骤 | 点群数 | 相似性水平 | 距离水平 | 已合并的点群号 | 新聚类号 | 新聚类号中的观测值个数 | |
|---|---|---|---|---|---|---|---|
| 1 | 4 | 93.9666 | 0.120669 | 2 | 3 | 2 | 2 |
| 2 | 3 | 93.1548 | 0.136904 | 4 | 5 | 4 | 2 |
| 3 | 2 | 87.3150 | 0.253700 | 1 | 4 | 1 | 3 |
| 4 | 1 | 79.8113 | 0.403775 | 1 | 2 | 1 | 5 |