平均值
如果采用类平均法,则两个聚类之间的距离等于一个聚类中的观测值与另一个聚类中的观测值之间的平均距离。该平均距离采用以下距离矩阵计算:

表示法
| 项 | 说明 |
|---|---|
| dmj | 聚类 m 和 j 之间的距离 |
| m | 由聚类 k 和 l 组成的合并聚类,其中 m = (k,i) |
| dkj | 聚类 k 和 j 之间的距离 |
| dlj | 聚类 l 和 j 之间的距离 |
| Nk | 聚类 k 中的观测值个数 |
| Nl | 聚类 l 中的观测值个数 |
| Nm | 聚类 m 中的观测值个数 |
质心
如果采用质心法,则两个聚类之间的距离等于聚类质心或均值之间的距离。该距离采用以下距离矩阵计算:
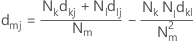
表示法
| 项 | 说明 |
|---|---|
| dmj | 聚类 m 和 j 之间的距离 |
| m | 由聚类 k 和 l 组成的合并聚类,其中 m = (k,i) |
| dkj | 聚类 k 和 j 之间的距离 |
| dlj | 聚类 l 和 j 之间的距离 |
| Nk | 聚类 k 中的观测值个数 |
| Nl | 聚类 l 中的观测值个数 |
| Nm | 聚类 m 中的观测值个数 |
最长距离法
如果采用最长距离法(亦称为最远邻接法),则两个聚类之间的距离等于一个聚类中的观测值与另一个聚类中的观测值之间的最大距离。最长距离采用以下距离矩阵计算:
dmj = max (dkj, dlj)
表示法
| 项 | 说明 |
|---|---|
| dmj | 聚类 m 和 j 之间的距离 |
| m | 由聚类 k 和 l 组成的合并聚类,其中 m = (k,i) |
| dkj | 聚类 k 和 j 之间的距离 |
| dlj | 聚类 l 和 j 之间的距离 |
简单平均
采用简单平均联结法,可使用以下距离矩阵计算距离:
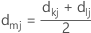
表示法
| 项 | 说明 |
|---|---|
| dmj | 聚类 m 和 j 之间的距离 |
| m | 由聚类 k 和 l 组成的合并聚类,其中 m = (k,i) |
| dkj | 聚类 k 和 j 之间的距离 |
| dlj | 聚类 l 和 j 之间的距离 |
中间距离法
如果选择中间距离法,则两个聚类之间的距离等于一个聚类中的观测值与另一个聚类中的观测值之间的中位数距离。该中位数距离采用以下距离矩阵计算:
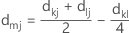
表示法
| 项 | 说明 |
|---|---|
| dmj | 聚类 m 和 j 之间的距离 |
| m | 由聚类 k 和 l 组成的合并聚类,其中 m = (k,i) |
| dkj | 聚类 k 和 j 之间的距离 |
| dlj | 聚类 l 和 j 之间的距离 |
| dkl | 聚类 k 和 l 之间的距离 |
最短距法
如果选择最短距法(也称为最近邻接法),则两个聚类之间的距离等于一个聚类中的观测值与另一个聚类中的观测值之间的最小距离。当观测值之间靠得很近时,最短距法往往会将它们识别为类似长链的聚类,这种聚类可以使用相对较大的距离来分隔链端处的观测值。
该距离采用以下距离矩阵计算:
dmj = min (dkj, dlj)
表示法
| 项 | 说明 |
|---|---|
| dmj | 聚类 m 和 j 之间的距离 |
| m | 由聚类 k 和 l 组成的合并聚类,其中 m = (k,i) |
| dkj | 聚类 k 和 j 之间的距离 |
| dlj | 聚类 l 和 j 之间的距离 |
Ward
如果采用 Ward 联结法,则两个聚类之间的距离等于点到质心的平方差之和。Ward 联结的目的是使聚类内平方和最小。该距离采用以下距离矩阵计算:
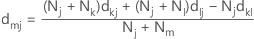
注意
如果采用 Ward 联结法,两个聚类之间的距离可以大于 dmax(原始距离矩阵 D 中的最大值)。如果发生这种情况,则相似性将为负值。
表示法
| 项 | 说明 |
|---|---|
| dmj | 聚类 m 和 j 之间的距离 |
| m | 由聚类 k 和 l 组成的合并聚类,其中 m = (k,i) |
| dkj | 聚类 k 和 j 之间的距离 |
| dlj | 聚类 l 和 j 之间的距离 |
| dkl | 聚类 k 和 l 之间的距离 |
| Nj | 聚类 j 中的观测值个数 |
| Nk | 聚类 k 中的观测值个数 |
| Nl | 聚类 l 中的观测值个数 |
| Nm | 聚类 m 中的观测值个数 |
